The monotonic correlation coefficients
The monotonic correlation may be described as monotonically increasing or monotonically decreasing. The relation between 2 features is presented by the monotonic increasing if the increasing of the one feature accompanies with the increasing of the other one. The relation between 2 features is presented by the monotonic decreasing if the increasing of the one feature accompanies with the decreasing of the other one.
The Spearman's rank-order correlation coefficient 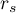 is used to describe the strength of monotonic relations between 2 features:
is used to describe the strength of monotonic relations between 2 features:  and
and  . It may be calculated on an ordinal scale or an interval one. The value of the Spearman's rank correlation coefficient should be calculated using the following formula:
. It may be calculated on an ordinal scale or an interval one. The value of the Spearman's rank correlation coefficient should be calculated using the following formula:
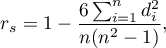
This formula is modified when there are ties:
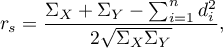
where:
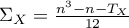 ,
, 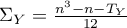 ,
,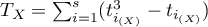 ,
, 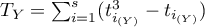 ,
, – number of cases included in tie.
– number of cases included in tie.
This correction is used, when ties occur. If there are no ties, the correction is not calculated, because the correction is reduced to the formula describing the above equation.
Note
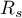 – the Spearman's rank correlation coefficient in a population;
– the Spearman's rank correlation coefficient in a population;
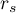 – the Spearman's rank correlation coefficient in a sample.
– the Spearman's rank correlation coefficient in a sample.
The value of 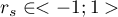 , and it should be interpreted the following way:
, and it should be interpreted the following way:
 means a strong positive monotonic correlation (increasing) – when the independent variable increases, the dependent variable increases too;
means a strong positive monotonic correlation (increasing) – when the independent variable increases, the dependent variable increases too;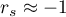 means a strong negative monotonic correlation (decreasing) – when the independent variable increases, the dependent variable decreases;
means a strong negative monotonic correlation (decreasing) – when the independent variable increases, the dependent variable decreases;- if the Spearman's correlation coefficient is of the value equal or very close to zero, there is no monotonic dependence between the analysed features (but there might exist another relation - a non monotonic one, for example a sinusoidal relation).
The Kendall's tau correlation coefficient (Kendall (1938)1)) is used to describe the strength of monotonic relations between features . It may be calculated on an ordinal scale or interval one. The value of the Kendall's 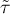 correlation coefficient should be calculated using the following formula:
correlation coefficient should be calculated using the following formula:
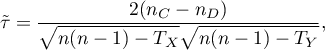
where:
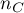 – number of pairs of observations, for which the values of the ranks for the
– number of pairs of observations, for which the values of the ranks for the  feature as well as
feature as well as  feature are changed in the same direction (the number of agreed pairs),
feature are changed in the same direction (the number of agreed pairs),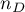 – number of pairs of observations, for which the values of the ranks for the
– number of pairs of observations, for which the values of the ranks for the  feature are changed in the different direction than for the
feature are changed in the different direction than for the  feature (the number of disagreed pairs),
feature (the number of disagreed pairs),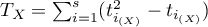 ,
, 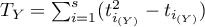 ,
, – number of cases included in a tie.
– number of cases included in a tie.
The formula for the 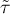 correlation coefficient includes the correction for ties. This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of
correlation coefficient includes the correction for ties. This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of 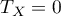 i
i 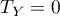 ) .
) .
Note
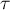 – the Kendall's correlation coefficient in a population;
– the Kendall's correlation coefficient in a population;
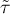 – the Kendall's correlation coefficient in a sample.
– the Kendall's correlation coefficient in a sample.
The value of  , and it should be interpreted the following way:
, and it should be interpreted the following way:
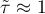 means a strong agreement of the sequence of ranks (the increasing monotonic correlation) – when the independent variable increases, the dependent variable increases too;
means a strong agreement of the sequence of ranks (the increasing monotonic correlation) – when the independent variable increases, the dependent variable increases too;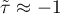 means a strong disagreement of the sequence of ranks (the decreasing monotonic correlation) – when the independent variable increases, the dependent variable decreases;
means a strong disagreement of the sequence of ranks (the decreasing monotonic correlation) – when the independent variable increases, the dependent variable decreases;- if the Kendall's
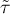 correlation coefficient is of the value equal or very close to zero, there is no monotonic dependence between analysed features (but there might exist another relation - a non monotonic one, for example a sinusoidal relation).
correlation coefficient is of the value equal or very close to zero, there is no monotonic dependence between analysed features (but there might exist another relation - a non monotonic one, for example a sinusoidal relation).
Spearman's versus Kendall's coefficient
- for an interval scale with a normality of the distribution, the
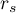 gives the results which are close to
gives the results which are close to 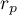 , but
, but 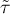 may be totally different from
may be totally different from 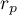 ,
, - the
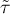 value is less or equal to
value is less or equal to 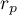 value,
value, - the
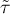 is an unbiased estimator of the population parameter
is an unbiased estimator of the population parameter 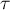 , while the
, while the 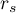 is a biased estimator of the population parameter
is a biased estimator of the population parameter 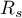 .
.
EXAMPLE cont. (sex-height.pqs file)
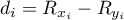 – difference of
– difference of  number of
number of 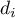 .
.