Spis treści
Testy parametryczne
Współczynnik korelacji wewnątrzklasowej i test badający jego istotność
Współczynnik korelacji wewnątrzklasowej (ang. ICC - intraclass correlation coefficient) stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonuje kilku „sędziów” ( ). Mierzy on siłę sędziowskiej rzetelności, czyli stopień w jakim ich oceny są zgodne.
). Mierzy on siłę sędziowskiej rzetelności, czyli stopień w jakim ich oceny są zgodne.
Ponieważ można go wyznaczać w kilku różnych sytuacjach, rozróżnia się kilka jego odmian zależnych od modelu i typu zgodności. W zależności od występującej w danych zmienności możemy rozróżnić 2 główne modele badań i 2 typy zgodności.
Model 1
Dla każdego z losowo wybranych  ocenianych obiektów, wybierany jest losowo zestaw
ocenianych obiektów, wybierany jest losowo zestaw  sędziów z populacji sędziów. Przy czym dla każdego obiektu inny zestaw
sędziów z populacji sędziów. Przy czym dla każdego obiektu inny zestaw  sędziów może być wylosowany. Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup niezależnych. Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(1,1) dany wzorem:
sędziów może być wylosowany. Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup niezależnych. Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(1,1) dany wzorem:
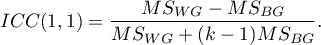
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(1,k) dany wzorem:
sędziów) wyznacza się ICC(1,k) dany wzorem:
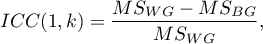
gdzie:
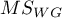 - średnia kwadratów wewnątrz grup,
- średnia kwadratów wewnątrz grup,
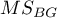 - średnia kwadratów między obiektami.
- średnia kwadratów między obiektami.
Model 2
Wybierany jest losowo zestaw  sędziów z populacji sędziów i każdy z nich ocenia wszystkie
sędziów z populacji sędziów i każdy z nich ocenia wszystkie  losowych obiektów.
Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup zależnych.
losowych obiektów.
Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup zależnych.
W zależności od poszukiwanego typu zgodności możemy szacować: zgodność bezwzględną tzn. jeśli sędziowie są zgodni bezwzględnie, to wydają dokładnie takie same oceny np. perfekcyjnie zgodne będą takie oceny wydane przez parę sędziów (2,2), (5,5), (8,8); lub spójność tzn. sędziowie mogą używać innych zakresów wartości ale poza tym przesunięciem nie powinno być różnic by zachować spójność werdyktu np. perfekcyjnie spójne będą takie oceny wydane przez parę sędziów (2,5), (5,8), (8,11).
- Zgodność bezwzględna
Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(2,1) dany wzorem:
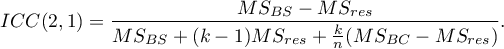
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(2,k) dany wzorem:
sędziów) wyznacza się ICC(2,k) dany wzorem:
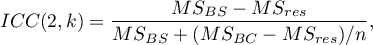
gdzie:
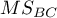 - średnia kwadratów między sędziami,
- średnia kwadratów między sędziami,
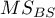 - średnia kwadratów między obiektami,
- średnia kwadratów między obiektami,
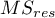 - średnia kwadratów dla reszt.
- średnia kwadratów dla reszt.
- Spójność
Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(2,1) dany wzorem:
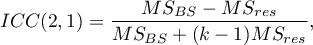
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(2,k) dany wzorem:
sędziów) wyznacza się ICC(2,k) dany wzorem:
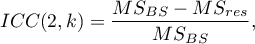
gdzie:
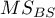 - średnia kwadratów między obiektami,
- średnia kwadratów między obiektami,
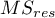 - średnia kwadratów dla reszt.
- średnia kwadratów dla reszt.
Uwaga!
Czasami istnieje konieczność rozważania modelu 3 1), tzn. wybierany jest zestaw  sędziów i każdy z nich ocenia wszystkie
sędziów i każdy z nich ocenia wszystkie  losowych obiektów. Wynik zgodności dotyczy tylko tych konkretnych
losowych obiektów. Wynik zgodności dotyczy tylko tych konkretnych  sędziów. Współczynnik ICC jest wówczas wyznaczany w modelu mieszanym (ponieważ losowość dotyczy tylko obiektów a nie dotyczy sędziów). Ponieważ ignorujemy zmienność dotyczącą sędziów, badamy spójność (a nie absolutną zgodność) i zastosowanie mogą mieć współczynniki z modelu drugiego: ICC(2,1) i ICC (2,k), gdyż są one tożsame z pożądanymi w tym przypadku współczynnikami ICC(3,1) i ICC (3,k) przy założeniu braku interakcji obiektów i sędziów.
sędziów. Współczynnik ICC jest wówczas wyznaczany w modelu mieszanym (ponieważ losowość dotyczy tylko obiektów a nie dotyczy sędziów). Ponieważ ignorujemy zmienność dotyczącą sędziów, badamy spójność (a nie absolutną zgodność) i zastosowanie mogą mieć współczynniki z modelu drugiego: ICC(2,1) i ICC (2,k), gdyż są one tożsame z pożądanymi w tym przypadku współczynnikami ICC(3,1) i ICC (3,k) przy założeniu braku interakcji obiektów i sędziów.
Uwaga!
Wartość 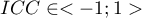 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
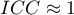 oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w dużej wariancji między obiektami (znacznej różnicy średnich między
oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w dużej wariancji między obiektami (znacznej różnicy średnich między  obiektami) i małej wariancji między ocenami sędziowskimi (niewielkiej różnicy średnich ocen wyznaczonych dla
obiektami) i małej wariancji między ocenami sędziowskimi (niewielkiej różnicy średnich ocen wyznaczonych dla  sędziów);
sędziów);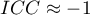 negatywny współczynnik korelacji wewnątrzklasowej, jest traktowany w ten sam sposób jak
negatywny współczynnik korelacji wewnątrzklasowej, jest traktowany w ten sam sposób jak 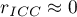 ;
;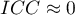 oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w małej wariancji między obiektami (niewielkiej różnicy średnich między
oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w małej wariancji między obiektami (niewielkiej różnicy średnich między  obiektami) i dużej wariancji między ocenami sędziowskimi (znaczącej różnicy średnich ocen wyznaczonych dla
obiektami) i dużej wariancji między ocenami sędziowskimi (znaczącej różnicy średnich ocen wyznaczonych dla  sędziów).
sędziów).
Test F do sprawdzania istotności współczynnika korelacji wewnątrzklasowej
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu dla wszystkich zmiennych będących różnicą par pomiarowych (lub normalność badanej zmiennej dla każdego pomiaru).
- dla modelu 1 - model niezależny, dla modelu 2 / 3 - model zależny.
Hipotezy:
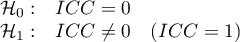
Statystyka testowa ma postać:
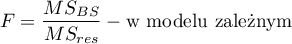
lub
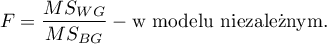
Statystyka ta podlega rozkładowi F Snedecora ze zdefiniowaną w modelu liczbą stopni swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji korelacji wewnątrzklasowej (ICC) wywołujemy poprzez menu Statystyka→Testy parametryczne→Korelacja wewnątrzklasowa (ICC) lub poprzez ''Kreator''.
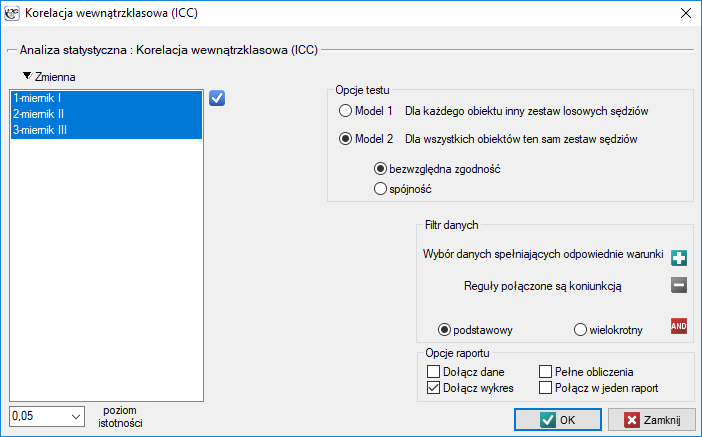
Przykład (plik natężenie dźwięku.pqs)
By skutecznie dbać o słuch pracowników zakładu pracy, w pierwszej kolejności należy rzetelnie oszacować natężenie dźwięku w poszczególnych miejscach przebywania osób. W pewnym zakładzie pracy postanowiono przed wyborem miernika natężenia dźwięku (sonografu) przeprowadzić eksperyment. Pomiarów natężenia dźwięku dokonano w 42 losowo wybranych na terenie zakładu punktach pomiarowych przy pomocy 3 wylosowanych sonografów analogowych i 3 losowo wybranych sonografów cyfrowych. Fragment zebranych pomiarów przedstawia poniższa tabela.
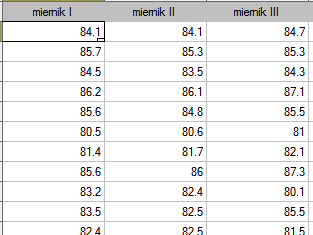
By sprawdzić który typ urządzenia (analogowy czy cyfrowy) lepiej zrealizuje postawione przed nim zadanie należy wyznaczyć współczynnik ICC w modelu 2 badając bezwzględną zgodność. Typ miernika o wyższym wskaźniku ICC będzie charakteryzował się bardziej wiarygodnymi pomiarami, przez co będzie w przyszłości wykorzystywany na terenie zakładu.
Analiza przeprowadzona dla mierników analogowych wskazuje na istotną zgodność pomiarów (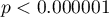 ). Rzetelność pomiaru dokonana miernikiem analogowym wynosi
). Rzetelność pomiaru dokonana miernikiem analogowym wynosi 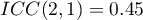 , natomiast rzetelność pomiaru będącego średnią pomiarów dokonanych przez 3 mierniki analogowe jest nieco wyższa i wynosi
, natomiast rzetelność pomiaru będącego średnią pomiarów dokonanych przez 3 mierniki analogowe jest nieco wyższa i wynosi 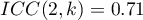 . Niepokojąco niska jest jednak dolna granica 95% przedziału ufności dla tych współczynników.
. Niepokojąco niska jest jednak dolna granica 95% przedziału ufności dla tych współczynników.
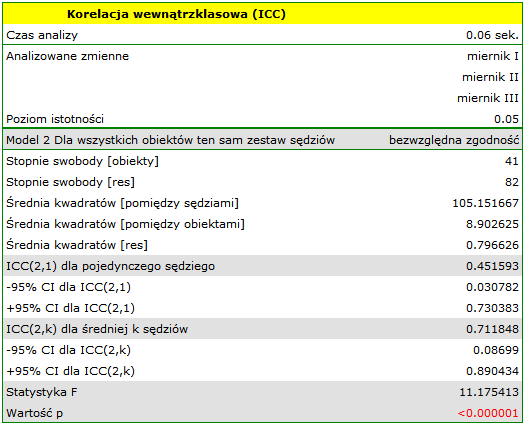
Podobna analiza przeprowadzona dla mierników cyfrowych dała lepsze rezultaty. Model ponownie jest istotny statystycznie, ale współczynniki ICC oraz ich przedziały ufności są znacznie wyżej niż dla mierników analogowych, a więc uzyskana zgodność bezwzględna jest wyższa 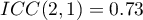 ,
, 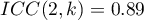 .
.
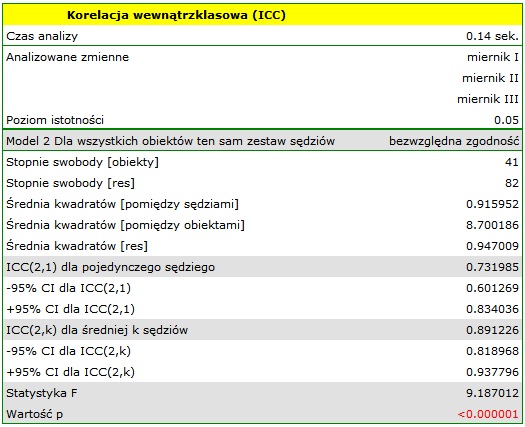
Dlatego ostatecznie w zakładzie pracy wykorzystywane będą mierniki cyfrowe.
Zgodność uzyskanych wyników dla mierników cyfrowych przedstawiono na wykresie punktowym, gdzie każdy punkt pomiarowy opisany jest wartością natężenia dźwięku uzyskaną dla poszczególnych mierników.
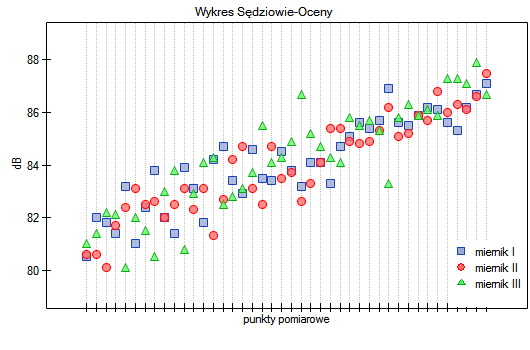
Przedstawiając wykres dla uprzednio posortowanych danych zgodnie ze średnią wartością natężenia dźwięku, można sprawdzić czy stopień zgodności rośnie lub spada wraz z wzrostem natężenia dźwięku. W przypadku naszych danych nieco wyższą zgodność (bliskość położenia punktów na wykresie) obserwować można przy wysokich wartościach natężenia dźwięku.
Podobnie, zgodność uzyskanych wyników obserwować można na wykresach Blanda-Altmana2) budowanych oddzielnie dla każdej pary mierników. Wykres dla miernika I i miernika II przedstawiono poniżej.
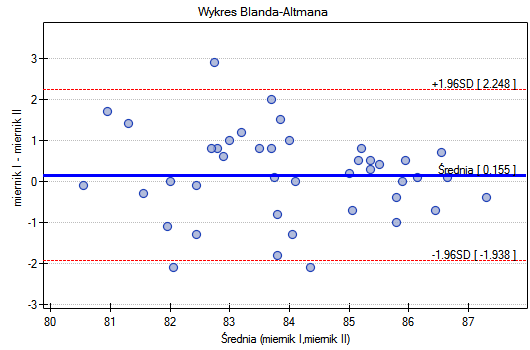
Tu również obserwujemy wyższą zgodność (punkty koncentrują się blisko osi poziomej y=0) dla wyższych wartości natężenia dźwięku.
Uwaga! Gdyby badaczowi nie zależało na oszacowaniu rzeczywistej wartości natężenia dźwięku na terenie zakładu, ale chciałby wskazać miejsca gdzie ten poziom jest wyższy niż w innych miejscach lub sprawdzić czy poziom hałasu zmienia się w czasie, wówczas wystarczającym modelem byłby model 2 badający spójność.
