Przykłady dla regresji logistycznej
Przeprowadzono badanie mające na celu identyfikację czynników ryzyka pewnej rzadko występującej wady wrodzonej u dzieci. W badaniu wzięło udział 395 matek dzieci z ta wadą oraz 375 matek dzieci zdrowych. Zebrane dane to: miejsce zamieszkania, płeć dziecka, masa urodzeniowa dziecka, wiek matki, kolejność ciąży, przebyte poronienia samoistne, infekcje oddechowe, palenie tytoniu, wykształcenie matki.
Budujemy model regresji logistycznej by sprawdzić które zmienne mogą wywierać istotny wpływ na występowanie wady. Jako zmienną zależną ustawiamy kolumnę GRUPA, wartością wyróżnioną w tej zmiennej jako  jest grupa
jest grupa badana, czyli matki dzieci z wadą wrodzoną. Kolejne 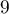 zmiennych, to zmienne niezależne:
zmiennych, to zmienne niezależne:
MiejsceZam (2=miasto/1=wieś),
Płeć (1=mężczyzna/0=kobieta),
MasaUr (w kilogramach z dokładnością do 0.5kg),
WiekM (w latach),
KolCiąży (dziecko z której ciąży),
PoronSamo (1=tak/0=nie),
InfOddech (1=tak/0=nie),
Palenie (1=tak/0=nie),
WyksztM (1=podstawowe lub niżej/2=zawodowe/3=średnie/4=wyższe).
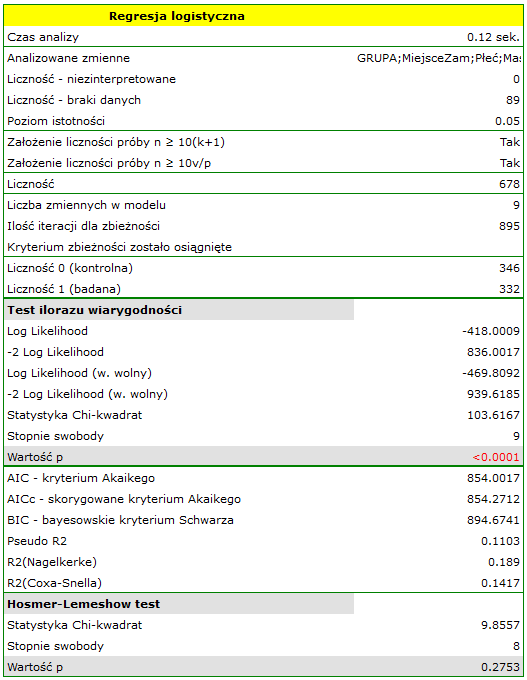
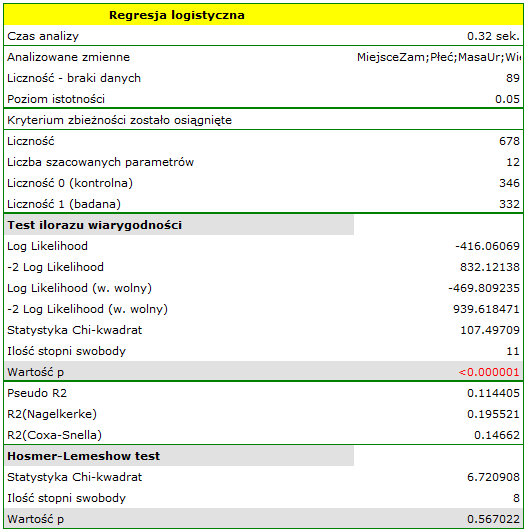
Jakość dopasowania modelu nie jest wysoka (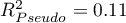 ,
, 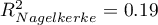 i
i 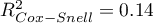 ). Jednocześnie model jest istotny statystycznie (wartość
). Jednocześnie model jest istotny statystycznie (wartość 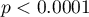 testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (
testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (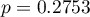 ). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
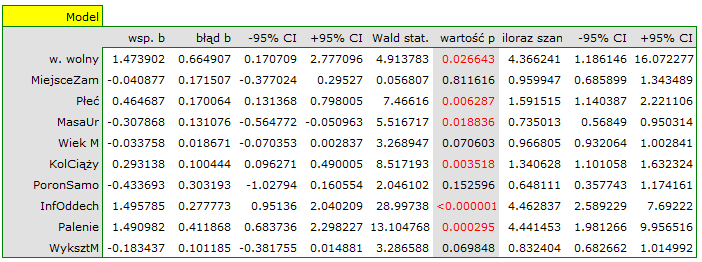
Interpretacja poszczególnych zmiennych w modelu zaczyna się od sprawdzenia ich istotności. W tym przypadku zmienne, które w istotny sposób są związane z występowaniem wady to:
Płeć: 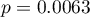 ,
,
MasaUr: 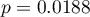 ,
,
KolCiąży: 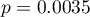 ,
,
InfOddech: 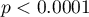 ,
,
Palenie: 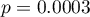 .
.
Badana wada wrodzona jest wadą rzadką, ale szansa na jej wystąpienie zależy od wymienionych zmiennych w sposób opisany poprzez iloraz szans:
- zmienna Płeć:
![LaTeX $OR[95\%CI]=1.60[1.14;2.22]$](/lib/exe/fetch.php?media=wiki:latex:/imgf8dc809d4d33fbf457e222bb2a246674.png) - szansa wystąpienia wady u chłopca jest
- szansa wystąpienia wady u chłopca jest 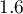 krotnie większa niż u dziewczynki;
krotnie większa niż u dziewczynki;
- zmienna MasaUr:
![LaTeX $OR[95\%CI]=0.74[0.57;0.95]$](/lib/exe/fetch.php?media=wiki:latex:/img5e023481fc641b1a88b75e8a1b4ba8be.png) - im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- zmienna KolCiąży:
![LaTeX $OR[95\%CI]=1.34[1.10;1.63]$](/lib/exe/fetch.php?media=wiki:latex:/imgbc4c66db7606d854bbbbe9db1cbb0a16.png) - szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą
- szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą 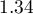 krotnie;
krotnie;
- zmienna InfOddech:
![LaTeX $OR[95\%CI]=4.46[2.59;7.69]$](/lib/exe/fetch.php?media=wiki:latex:/imga1c2b1a351fce6107ff7c7ccc044c83d.png) - szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest
- szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest 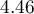 krotnie większa niż gdyby jej nie przechodziła;
krotnie większa niż gdyby jej nie przechodziła;
- zmienna Palenie:
![LaTeX $OR[95\%CI]=4.44[1.98;9.96]$](/lib/exe/fetch.php?media=wiki:latex:/img14fd8b0c97c85092641099b3a0c857d8.png) - matka paląca w czasie ciąży zwiększa
- matka paląca w czasie ciąży zwiększa 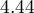 krotnie szansę na wystąpienia wady u dziecka
krotnie szansę na wystąpienia wady u dziecka
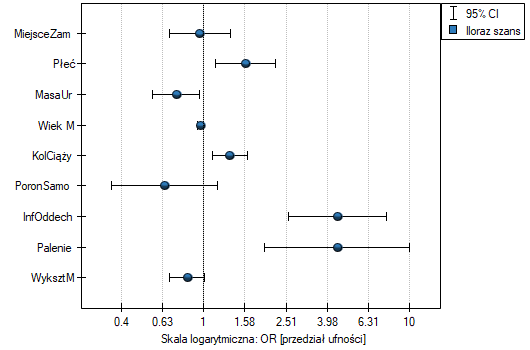
W przypadku zmiennych nieistotnych statystycznie przedział ufności dla Ilorazu Szans zawiera jedynkę co oznacza, że zmienne te nie zwiększają ani nie zmniejszają szansy na wystąpienie badanej wady. Nie można więc interpretować uzyskanego ilorazu w podobny sposób jak dla zmiennych istotnych statystycznie.
Wpływ poszczególnych zmiennych niezależnych na występowanie wady możemy równiez opisać przy pomocy wykresu dotyczącego ilorazu szans:
Przykład c.d. (wada.pqs)
Zbudujemy raz jeszcze model regresji logistycznej, ale tym razem zmienną wykształcenie rozbijemy na zmienne fikcyjne (kodowanie zero-jedynkowe). Tracimy tym samym informację o uporządkowaniu kategorii wykształcenia, ale zyskujemy możliwość wnikliwszej analizy poszczególnych kategorii. Rozbicia na zmienne fikcyjne dokonujemy wybierając w oknie analizy Zm. fikcyjne:
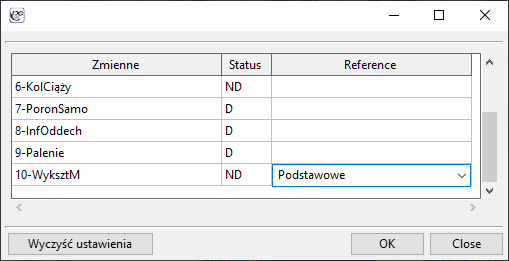
Wykształcenie podstawowe wybieramy jako kategorię odniesienia.
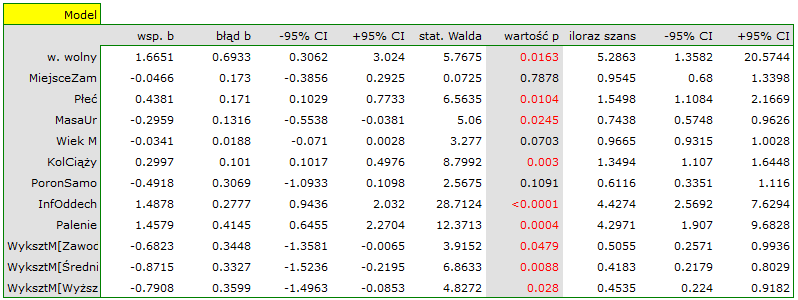
W rezultacie zmienne opisujące wykształcenie stają się istotne statystycznie. Dopasowanie modelu nie ulega znacznej zmianie, ale zmienia się sposób interpretacji ilorazu szans dla wykształcenia:
![LaTeX \begin{tabular}{|l|l|}
\hline
\textbf{Zmienna}& $OR[95\%CI]$ \\\hline
Wykształcenie podstawowe& kategoria referencyjna\\
Wykształcenie zawodowe& $0.51[0.26;0.99]$\\
Wykształcenie średnie& $0.42[0.22;0.80]$\\
Wykształcenie wyższe& $0.45[0.22;0.92]$\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img293c66232b211018957d259498fcf4db.png)
Szansa na wystąpienie badanej wady w każdej kategorii wykształcenia odnoszona jest zawsze do szansy wystąpienia wady przy wykształceniu podstawowym. Widzimy, że dla bardziej wykształconych matek, iloraz szans jest niższy. Dla matki z wykształceniem:
- zawodowym szansa wystąpienia wady u dziecka stanowi 0.51 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- średnim szansa wystąpienia wady u dziecka stanowi 0.42 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- wyższym szansa wystąpienia wady u dziecka stanowi 0.45 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym.
Przeprowadzono eksperyment mający na celu zbadanie umiejętność koncentracji grupy dorosłych podczas sytuacji niekomfortowych. W eksperymencie wzięło udział 190 osób (130 osób to zbiór uczący, 40 osób to zbiór testowy). Każda badana osoba dostała pewne zadanie, którego rozwiązanie wymagało skupienia uwagi. Podczas eksperymentu niektóre osoby zostały poddane działaniu czynnika zakłócającego jakim była podwyższona temperatura powietrza do 32 stopni Celsiusza. Osoby biorące udział w eksperymencie zapytano dodatkowo o ich miejsce zamieszkania, płeć, wiek i wykształcenie. Czas na rozwiązanie zadania ograniczono do 45 minut. Dla osób, które skończyły przed czasem odnotowano rzeczywisty czas poświęcony na rozwiązanie. Całość naszych obliczeń wykonamy tylko dla osóbnależących do zbioru uczącego.
Zmienna ROZWIĄZANIE (tak/nie) zawiera wynik eksperymentu, czyli informację o tym, czy zadanie zostało rozwiązane poprawnie czy też nie. Pozostałe zmienne, które mogły wpływać na wynik eksperymentu to:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Na bazie wszystkich zmiennych zbudowano model regresji logistycznej, gdzie jako stan wyróżniony zmiennej ROZWIĄZANIE wybrano tak.
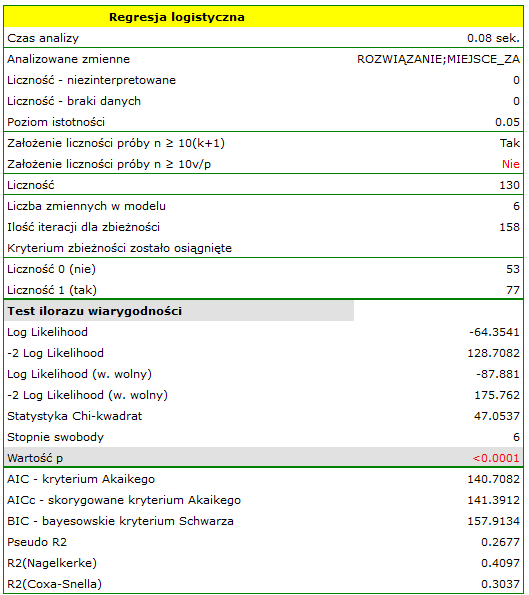
Jakość jego dopasowania opisują współczynniki: 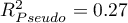 ,
, 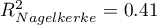 i
i  . Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa
. Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa 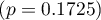 . Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności
. Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności 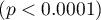 .
.
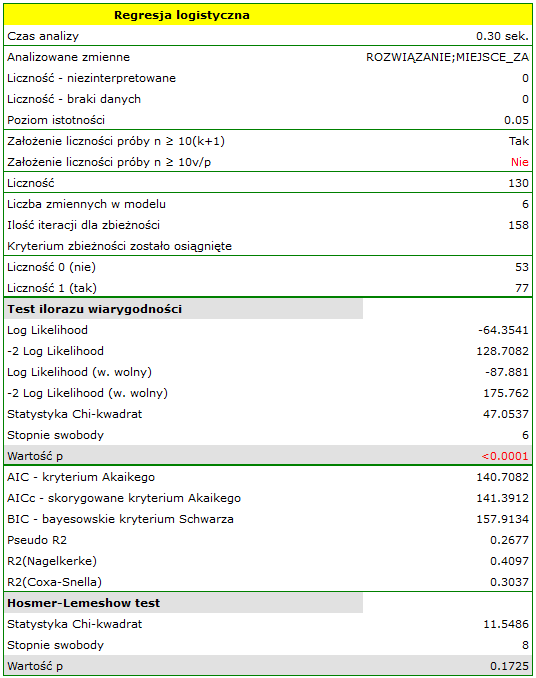
Wartości obserwowane i prawdopodobieństwo przewidywane możemy zobaczyć na wykresie:
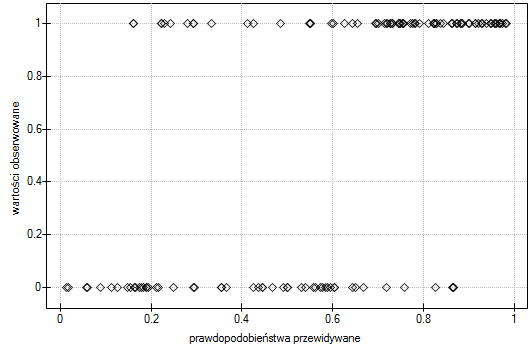
W modelu zmienne, które w sposób istotny wpływają na wynik to:
WIEK: 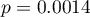 ,
,
CZAS: 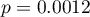 ,
,
ZAKŁÓCENIA: 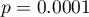 .
.
Przy czym, im osoba rozwiązująca jest młodsza, czas rozwiązywania krótszy i brak jest czynnika zakłócającego, tym większe prawdopodobieństwo poprawnego rozwiązania:
WIEK: ![LaTeX $OR[95\%CI]=0.90[0.85;0.96]$](/lib/exe/fetch.php?media=wiki:latex:/img2d561911e46044388c920f350283e92f.png) ,
,
CZAS: ![LaTeX $OR[95\%CI]=0.91[0.87;0.97]$](/lib/exe/fetch.php?media=wiki:latex:/img856be89e1314daa3623408b907f11c45.png) ,
,
ZAKŁÓCENIA: ![LaTeX $OR[95\%CI]=0.15[0.06;0.37]$](/lib/exe/fetch.php?media=wiki:latex:/img8cb35d4670d9bda19bc8f3dd46b985b3.png) .
.
Uzyskane wyniki Ilorazu Szans przedstawiono na poniższym wykresie:
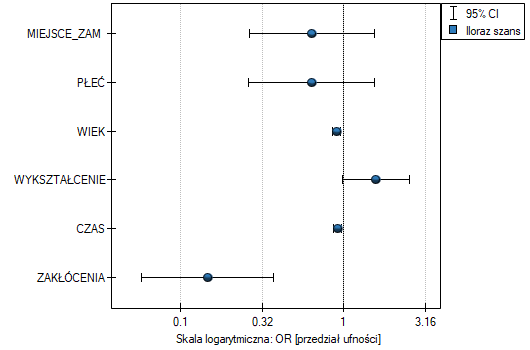
Jeśli model miałby zostać użyty do prognozowania, to należy przyjrzeć się jakości klasyfikacji. Wyliczamy w tym celu krzywe ROC.
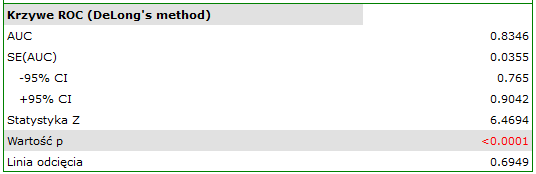
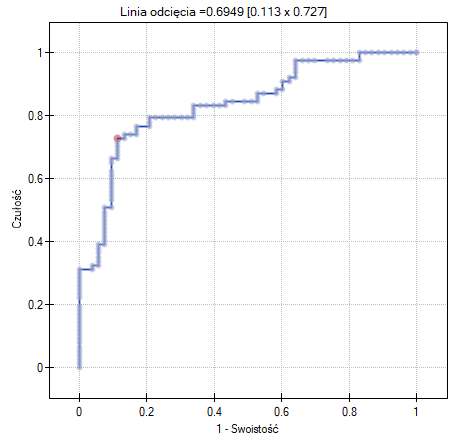
Rezultat wydaje się zadowalający. Pole pod krzywą wynosi 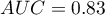 i jest istotnie większe niż
i jest istotnie większe niż 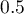
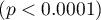 , więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi
, więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi 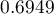 i jest nieco wyższy niż standardowo używany w regresji poziom
i jest nieco wyższy niż standardowo używany w regresji poziom 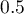 . Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
. Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
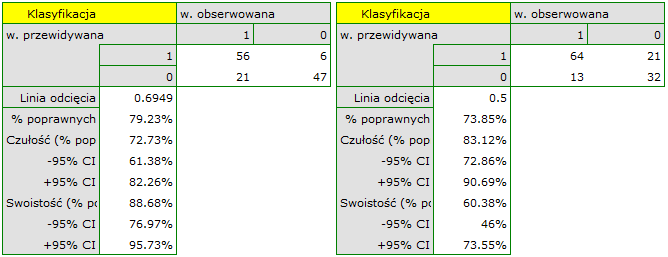
Na tym etapie możemy zakończyć analizę klasyfikacji, lub jeśli wynik nie jest wystarczający bardziej wnikliwą analizę krzywej ROC możemy przeprowadzić w module Krzywa ROC.
Ponieważ uznaliśmy, że klasyfikacja na podstawie modelu jest zadowalająca, możemy wyliczyć prognozowaną wartość zmiennej zależnej dla dowolnie zadanych warunków. Sprawdźmy jakie szanse na rozwiązanie zadania ma osoba dla której:
MIEJSCEZAM (1=miasto),
PŁEĆ (1=kobieta),
WIEK (50 lat),
WYKSZTAŁCENIE (1=podstawowe),
CZAS rozwiązywania (20 minut),
ZAKŁÓCENIA (1=tak).
W tym celu na podstawie wartości współczynnika  wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi
wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi tak pod warunkiem określenia wartości zmiennych zależnych):
![LaTeX \begin{displaymath}
\begin{array}{l}
P(Y=tak|MIEJSCEZAM,PŁEĆ,WIEK,WYKSZTAŁCENIE,CZAS,ZAKŁÓCENIA)=\\[0.2cm]
=\frac{e^{7.23-0.45\textrm{\scriptsize \textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}{1+e^{7.23-0.45\textrm{\scriptsize\textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}=\\[0.2cm]
=\frac{e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}{1+e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img05c978955ec4691a8e7bfe3d265dc858.png)
W rezultacie tych obliczeń program zwróci wynik:
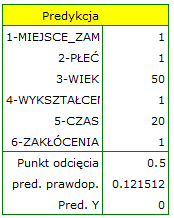
Uzyskane prawdopodobieństwo rozwiązania zadania wynosi 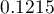 , więc na podstawie punktu odcięcia
, więc na podstawie punktu odcięcia 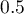 przewidziany wynik to
przewidziany wynik to  - czyli zadanie nie rozwiązane poprawnie.
- czyli zadanie nie rozwiązane poprawnie.