en:statpqpl:wielowympl:mediacja

Mediation effect

Baron and Kenny (1986)¹⁾ defined a mediator (M) as a variable that significantly explains the relationship between the independent variable (X) and the outcome variable (Y). In mediation, the relationship between the independent variable and the dependent variable is assumed to be an indirect effect that exists due to the influence of a third variable (mediator).

$\begin{pspicture}(-0.5,-0.5)(4,3.5) \psline{->}(0.2,3)(2.8,3) \rput(-2,3){\scriptsize one-dimensional model} \rput(0,2.8){\scriptsize \textbf{X}} \rput(3,2.8){\scriptsize \textbf{Y}} \rput(1.5,2.7){\scriptsize $\tau$} \rput(-2,0){\scriptsize multidimensional model} \rput(0,0){\scriptsize \textbf{X}} \rput(3,0){\scriptsize \textbf{Y}} \rput(1.5,2){\scriptsize \textbf{M}} \psline[linewidth=0.7pt, linestyle=dotted]{->}(0.2,0.2)(1.2,1.8) \psline[linewidth=0.7pt, linestyle=dotted]{->}(1.8,1.8)(2.8,0.2) \psline{->}(0.2,0)(2.8,0) \rput(0.4,1){\scriptsize \textit{a}} \rput(2.6,1){\scriptsize \textit{b}} \rput(1.5,-0.2){\scriptsize $\tau'$} \end{pspicture}$

We determine the magnitude of change by the difference in the coefficients describing the relationship between variable X and variable Y in the univariate model:

$Y=\tau\cdot X+c$

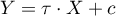
and in the multivariate model, that is, including the variable M:

$Y=\tau\cdot X+b\cdot M+c$ .

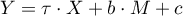Difference:

$\begin{displaymath} \tau-\tau'=a\cdot b \end{displaymath}$

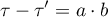
Mediation effect:

$\begin{displaymath} \frac{\tau-\tau'}{\tau}\cdot 100\% \end{displaymath}$

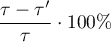
As a result, when the mediator (M) is included in the regression model that determines the relationship between the variable X and Y, the influence of the independent variable 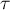$\tau$ is reduced to $\tau'$ .

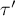Tests to evaluate the mediation effect

The Sobel (1982)²⁾ test, the Aroian (1947)³⁾ test popularized by Baron and Kenny ⁴⁾, and the Goodman (1960)⁵⁾ test are tests that determine whether the reduction in the effect of the independent variable on the outcome variable, when a mediator is included in the model, is a significant reduction and therefore whether the mediation effect is statistically significant.

Hypotheses:

$\begin{array}{cl} \mathcal{H}_0: & \tau = \tau'\\ \mathcal{H}_1: & \tau \ne \tau', \end{array}$

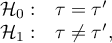
The test statistic for the Sobel test has the form:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b}} \end{displaymath}$

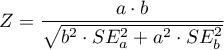
The test statistic for the Aroian test has the form:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b + SE^2_a\cdot SE^2_b}} \end{displaymath}$

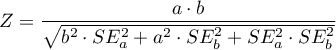
The test statistic for the Goodman test has the form:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b - SE^2_a\cdot SE^2_b}} \end{displaymath}$

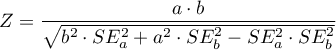
These statistics have an asymptotically (for large sizes) normal distribution.

The p-value, designated on the basis of the test statistic, is compared with the significance level $\alpha$ :

$\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}$

Note

The Sobel test, as well as the Aroian and Goodman test, are very conservative tests and are intended only for large samples (greater than 100 items).

The mediation effect analysis window is invoked by Advanced Statistics→Multidivariate models→Mediation effect.

EXAMPLE

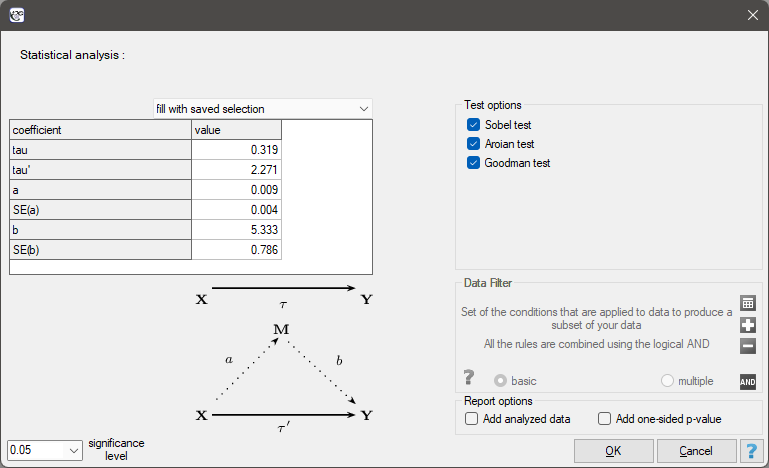
Based on the paper by Mimar Sinan Fine (2017) ⁶⁾.

The study includes 300 adults living in Istanbul. The dependent variable Y is systolic blood pressure and the independent variable X is age. The mediating variable M is the frequency of alcohol consumption. The purpose of this study is to investigate the relationship between age and systolic blood pressure and to present the effect of frequency of alcohol consumption on this relationship.

A one-dimensional model was built that did not account for the potential mediator:

$Y=0.319 \cdot X+c$ .

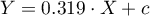The effect size of variable X (age) on variable Y (systolic blood pressure) was tau=0.319.

A one-dimensional model was constructed that did not include a potential mediator:

The effect size of variable X (age) on variable Y (systolic blood pressure) was tau'=2.271. We also know from this model that b=5.333, and error 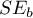$SE_b$ =0.786

The difference between the coefficients is tau-tau'= a*b=0.048. The effect of mediation is (tau-tau')/tau=(0.319-0.271)/0.371=0.15047, which means that M (frequency of alcohol consumption) modifies the relationship under study by decreasing the coefficient by about 15%.

A one-dimensional model was built to examine the effect of variable X on the mediator:

$M=0.009\cdot X+c$ .

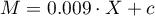We know from this model that the coefficient a=0.009, and the error 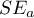$SE_a$ =0.004. We enter all this information in the analysis window obtaining the following report:

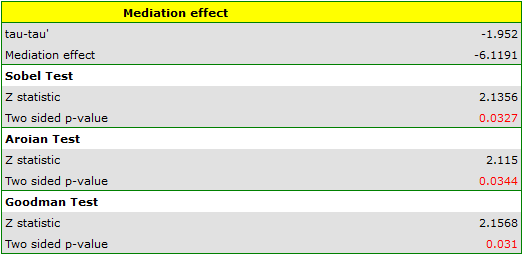
Based on the coefficients a and b and their standard errors, the result of Sobel (p=0.0327), Aroian (p=0.0344) and Goodman (p=0.0310) tests are determined. The obtained p-values indicate a statistically significant mediator. Thus, we confirmed that frequency of alcohol consumption affects the association of age with diastolic blood pressure so noticeably that it is worth explaining why this effect occurs.

¹⁾ , ⁴⁾

Baron R. M., Kenny D. A. (1986), The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology, 51, 1173-1182.

²⁾

Sobel M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology 13: 290–312

³⁾

Aroian, L. A. (1947), The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics, 18, 265-271.

⁵⁾

Goodman L. A. (1960), On the exact variance of products. Journal of the American Statistical Association, 55, 708-713

⁶⁾

Mimar S.F. (2017), The Mediation Analysis With the Sobel Test and the Percentile Bootstrap, International Journal of Management and Applied Science, Volume-3, Issue-2