Model verification
- Statistical significance of particular variables in the model (significance of the Odds Ratio)
On the basis of the coefficient and its error of estimation we can infer if the independent variable for which the coefficient was estimated has a significant effect on the dependent variable. For that purpose we use Wald test.
Hypotheses:
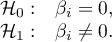
or, equivalently:
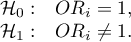
The Wald test statistics is calculated according to the formula:
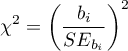
The statistic asymptotically (for large sizes) has the Chi-square distribution with  degree of freedom.
degree of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

- The quality of the constructed model
A good model should fulfill two basic conditions: it should fit well and be possibly simple. The quality of multiple linear regression can be evaluated can be evaluated with a few general measures based on:
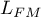 - the maximum value of likelihood function of a full model (with all variables),
- the maximum value of likelihood function of a full model (with all variables),
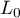 - the maximum value of the likelihood function of a model which only contains one free word,
- the maximum value of the likelihood function of a model which only contains one free word,
 - the sample size.
- the sample size.
- Information criteria are based on the information entropy carried by the model (model insecurity), i.e. they evaluate the lost information when a given model is used to describe the studied phenomenon. We should, then, choose the model with the minimum value of a given information criterion.
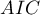 ,
, 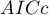 , and
, and 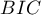 is a kind of a compromise between the good fit and complexity. The second element of the sum in formulas for information criteria (the so-called penalty function) measures the simplicity of the model. That depends on the number of variables (
is a kind of a compromise between the good fit and complexity. The second element of the sum in formulas for information criteria (the so-called penalty function) measures the simplicity of the model. That depends on the number of variables ( ) in the model and the sample size (
) in the model and the sample size ( ). In both cases the element grows with the increase of the number of variables and the growth is the faster the smaller the number of observations.
The information criterion, however, is not an absolute measure, i.e. if all the compared models do not describe reality well, there is no use looking for a warning in the information criterion.
). In both cases the element grows with the increase of the number of variables and the growth is the faster the smaller the number of observations.
The information criterion, however, is not an absolute measure, i.e. if all the compared models do not describe reality well, there is no use looking for a warning in the information criterion.
- Akaike information criterion
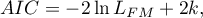
It is an asymptomatic criterion, appropriate for large sample sizes.
- Corrected Akaike information criterion
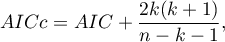
Because the correction of the Akaike information criterion concerns the sample size it is the recommended measure (also for smaller sizes).
- Bayesian information criterion or Schwarz criterion
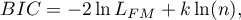
Just like the corrected Akaike criterion it takes into account the sample size.
- Pseudo R
 - the so-called McFadden R
- the so-called McFadden R is a goodness of fit measure of the model (an equivalent of the coefficient of multiple determination
is a goodness of fit measure of the model (an equivalent of the coefficient of multiple determination 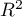 defined for multiple linear regression).
defined for multiple linear regression).
The value of that coefficient falls within the range of 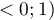 , where values close to 1 mean excellent goodness of fit of a model,
, where values close to 1 mean excellent goodness of fit of a model, 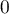 - a complete lack of fit Coefficient
- a complete lack of fit Coefficient 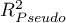 is calculated according to the formula:
is calculated according to the formula:
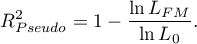
As coefficient 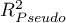 never assumes value 1 and is sensitive to the amount of variables in the model, its corrected value is calculated:
never assumes value 1 and is sensitive to the amount of variables in the model, its corrected value is calculated:
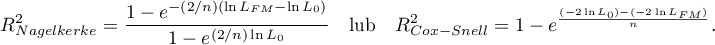
- Statistical significance of all variables in the model
The basic tool for the evaluation of the significance of all variables in the model is the Likelihood Ratio test. The test verifies the hypothesis:
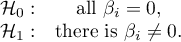
The test statistic has the form presented below:
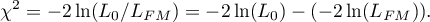
The statistic asymptotically (for large sizes) has the Chi-square distribution with  degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

- Hosmer-Lemeshow test - The test compares, for various subgroups of data, the observed rates of occurrence of the distinguished value
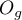 and the predicted probability
and the predicted probability 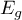 . If
. If 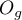 and
and 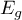 are close enough then one can assume that an adequate model has been built.
are close enough then one can assume that an adequate model has been built.
For the calculation the observations are first divided into 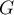 subgroups - usually deciles (
subgroups - usually deciles (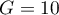 ).
).
Hypotheses:
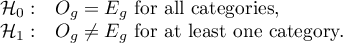
The test statistic has the form presented below:
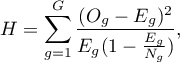
where:
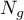 - the number of observations in group
- the number of observations in group 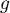 .
.
The statistic asymptotically (for large sizes) has the Chi-square distribution with 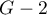 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

- AUC - the area under the ROC curve - The ROC curve built on th ebasis of the value of the dependent variable, and the predicted probability of dependent variable
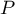 , allows to evaluate the ability of the constructed logistic regression model to classify the cases into two groups: (1) and (0). The constructed curve, especially the area under the curve, presents the classification quality of the model. When the ROC curve overlaps with the diagonal
, allows to evaluate the ability of the constructed logistic regression model to classify the cases into two groups: (1) and (0). The constructed curve, especially the area under the curve, presents the classification quality of the model. When the ROC curve overlaps with the diagonal  , then the decision about classifying a case within a given class (1) or (0), made on the basis of the model, is as good as a random division of the studied cases into the groups. The classification quality of a model is good when the curve is much above the diagonal
, then the decision about classifying a case within a given class (1) or (0), made on the basis of the model, is as good as a random division of the studied cases into the groups. The classification quality of a model is good when the curve is much above the diagonal  , that is when the area under the ROC curve is much larger than the area under the
, that is when the area under the ROC curve is much larger than the area under the  line, i.e. it is greater than
line, i.e. it is greater than 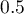
Hypotheses:
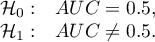
The test statistic has the form presented below:
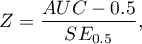
where:
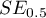 - area error.
- area error.
Statistics  asymptotically (for large sizes) has the normal distribution.
asymptotically (for large sizes) has the normal distribution.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Additionally, for ROC curve the suggested value of the cut-off point of the predicted probability is given, together with the table of sensitivity and specificity for each possible cut-off point.
Note!
More possibilities of calculating a cut-off point are offered by module **ROC curve**. The analysis is made on the basis of observed values and predicted probability obtained in the analysis of Logistic Regression.
- Classification
On the basis of the selected cut-off point of predicted probability we can change the classification quality. By default the cut-off point has the value of 0.5. The user can change the value into any value from the range of 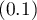 , e.g. the value suggested by the ROC curve.
, e.g. the value suggested by the ROC curve.
As a result we shall obtain the classification table and the percentage of properly classified cases, the percentage of properly classified (0) - specificity, and the percentage of properly classified (1) - sensitivity.