The Fisher-Snedecor test

The F-Snedecor test is based on a variable 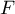$F$ which was formulated by Fisher (1924), and its distribution was described by Snedecor. This test is used to verify the hypothesis about equality of variances of an analysed variable for 2 populations.

Basic assumptions:

Hypotheses:

\begin{array}{cc} \mathcal{H}_0: & \sigma_1^2=\sigma_2^2,\\ \mathcal{H}_1: & \sigma_1^2\ne\sigma_2^2, \end{array}

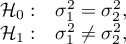
where:

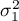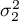$\sigma_1^2$, $\sigma_2^2$ – variances of an analysed variable of the 1st and the 2nd population.

The test statistic is defined by: \begin{displaymath} F=\displaystyle{\frac{sd_1^2}{sd_2^2}}, \end{displaymath}

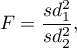
where:

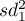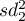$sd_1^2$, $sd_2^2$ – variances of an analysed variable of the samples chosen randomly from the 1st and the 2nd population.

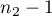The test statistic has the F Snedecor distribution with $n_1-1$ and $n_2-1$ degrees of freedom.

The p-value, designated on the basis of the test statistic, is compared with the significance level $\alpha$:

\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}

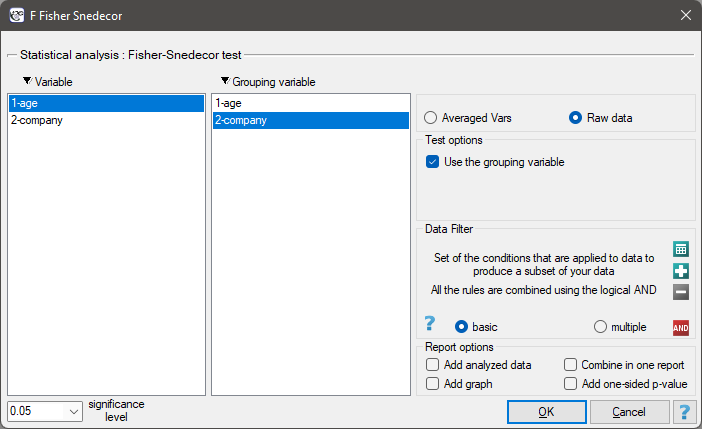
The settings window with the Fisher-Snedecor test can be opened in Statistics menu→Parametric tests→F Fisher Snedecor.

Note

Calculations can be based on raw data or data that are averaged like: arithmetic means, standard deviations and sample sizes.