Poprawki testu chi-kwadrat dla małych tabel
Testy te opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których każda ma możliwe 2 kategorie
), z których każda ma możliwe 2 kategorie 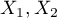 oraz
oraz 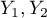 .
.
Test chi-kwadrat z poprawką Yatesa na ciągłość
Test  z poprawką Yatesa (ang. Chi-square test with Yates correction), Frank Yates (1934)1) jest testem bardziej konserwatywny od testu chi-kwadrat (trudniej niż test chi-kwadrat odrzuca hipotezę zerową). Poprawka na ciągłość ma zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu chi-kwadrat.
z poprawką Yatesa (ang. Chi-square test with Yates correction), Frank Yates (1934)1) jest testem bardziej konserwatywny od testu chi-kwadrat (trudniej niż test chi-kwadrat odrzuca hipotezę zerową). Poprawka na ciągłość ma zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu chi-kwadrat.
Statystyka testowa ma postać:
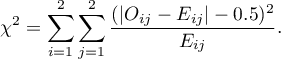
Test Fishera dla tabel 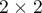 nazywany jest również testem dokładnym Fishera (ang. Fisher exact test), R. A. Fisher (19342), 19353)). Test ten określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym
nazywany jest również testem dokładnym Fishera (ang. Fisher exact test), R. A. Fisher (19342), 19353)). Test ten określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym  i ustalonych sumach brzegowych.
i ustalonych sumach brzegowych.
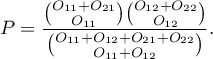 Przy znanych sumach brzegowych, dla różnych układów wartości obserwowanych wyznaczamy prawdopodobieństwa
Przy znanych sumach brzegowych, dla różnych układów wartości obserwowanych wyznaczamy prawdopodobieństwa 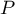 . Dokładny poziom istotności
. Dokładny poziom istotności  jest sumą tych prawdopodobieństw, które są mniejsze lub równe badanemu prawdopodobieństwu.
jest sumą tych prawdopodobieństw, które są mniejsze lub równe badanemu prawdopodobieństwu.
mid-p jest korektą testu dokładnego Fishera. Ta zmodyfikowana wartość  jest rekomendowana przez wielu statystyków (Lancaster 19614), Anscombe 19815), Pratt i Gibbons 19816), Plackett 19847), Miettinen 19858) i Barnard 19899), Rothman 200810)) jako metoda zmniejszenia konserwatyzm testu dokładnego Fishera. W rezultacie testem mid-p szybciej odrzucimy hipotezę zerowa niż dokładnym testem Fishera. Dla dużych prób wartość
jest rekomendowana przez wielu statystyków (Lancaster 19614), Anscombe 19815), Pratt i Gibbons 19816), Plackett 19847), Miettinen 19858) i Barnard 19899), Rothman 200810)) jako metoda zmniejszenia konserwatyzm testu dokładnego Fishera. W rezultacie testem mid-p szybciej odrzucimy hipotezę zerowa niż dokładnym testem Fishera. Dla dużych prób wartość  otrzymana przy pomocy testu
otrzymana przy pomocy testu  z poprawką Yatesa i test Fishera dają zbliżone wyniki, natomiast wartość
z poprawką Yatesa i test Fishera dają zbliżone wyniki, natomiast wartość  testu
testu  bez korekcji koresponduje z wartością mid-p.
bez korekcji koresponduje z wartością mid-p.
Wartość  mid-p wyznaczana jest przez przekształcenie wartości prawdopodobieństwa dla testu dokładnego Fishera. Jednostronna wartość
mid-p wyznaczana jest przez przekształcenie wartości prawdopodobieństwa dla testu dokładnego Fishera. Jednostronna wartość  wyznaczana jest ze wzoru:
wyznaczana jest ze wzoru:
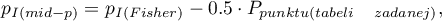
gdzie:
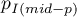
 wartość jednostronna
wartość jednostronna  testu mid-p
testu mid-p
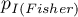
 wartość jednostronna
wartość jednostronna  testu dokładnego Fishera
testu dokładnego Fishera
a dwustronna wartość  jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw:
jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw:
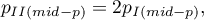
gdzie:
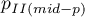
 wartość dwustronna
wartość dwustronna  testu mid-p.
testu mid-p.
