Testowanie hipotez

Weryfikacja hipotez statystycznych, to sprawdzanie określonych założeń sformułowanych dla parametrów populacji generalnej na podstawie wyników z próby.

Sformułowanie hipotez, które będą weryfikowane za pomocą testów statystycznych.

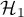Każdy test statystyczny podaje postać ogólną hipotezy zerowej - $\mathcal{H}_0$(ang. null hypothesis) i alternatywnej - $\mathcal{H}_1$ (ang. alternative hypothesis):

\begin{array}{cl} \mathcal{H}_0: & \textrm{\textbf{w badanej populacji} \textcolor{red}{\textbf{NIE MA}} ważnej statystycznie}\\ &\textrm{\quad np. zależności},\\ &\textrm{\quad np. różnicy},\\ &\textrm{\quad ...}\\ &\textrm{\textbf{między}}\\ &\textrm{\quad np. rozkładem przestrzennym},\\ &\textrm{\quad np. występowaniem poszczególnych wartości},\\ &\textrm{\quad ...}\\ &\textrm{\textbf{w analizowanym obszarze}},\\\\ \mathcal{H}_1: & \textrm{\textbf{w badanej populacji} \textcolor{red}{\textbf{ISTNIEJE}} ważna statystycznie}\\ &\textrm{\quad np. zależności},\\ &\textrm{\quad np. różnicy},\\ &\textrm{\quad ...}\\ &\textrm{\textbf{między}}\\ &\textrm{\quad np. rozkładem przestrzennym},\\ &\textrm{\quad np. występowaniem poszczególnych wartości},\\ &\textrm{\quad ...}\\ &\textrm{\textbf{w analizowanym obszarze}}.\\\\ \end{array}

Przykład:

\begin{array}{cl} \mathcal{H}_0: & \textrm{NIE MA ważnej statystycznie zależności między rozkładem przestrzennym}\\ &\textrm{sklepów chemicznych w Wielkopolsce - zakładamy, że ich rozkład na }\\ &\textrm{badanym obszarze jest losowy}.\\ \end{array}

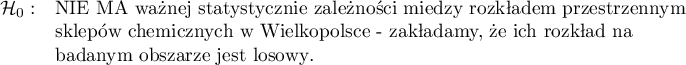
Jeśli nie wiemy, czy rozkład sklepów może być bardziej regularny niż rozkład losowy czy też też odwrotnie - bardziej skupiony niż rozkład losowy, wówczas hipoteza alternatywna powinna być dwustronna, tzn. nie zakładamy kierunku:

\begin{array}{cl} \mathcal{H}_1: & \textrm{ISTNIEJE ważna statystycznie zależność między rozkładem przestrzennym}\\ &\textrm{sklepów chemicznych w Wielkopolsce - zakładamy, że ich rozkład na }\\ &\textrm{badanym obszarze jest nielosowy, czyli zakładamy 2 kierunki: rozkład}\\ &\textrm{bardziej regularny niż losowy i rozkład bardziej skupiony niż losowy}.\\ \end{array}

Może się zdarzyć (są to bardzo rzadkie przypadki), że mamy pewność, iż znamy kierunek w hipotezie alternatywnej. Wówczas można zastosować jednostronną hipotezę alternatywną.

Weryfikacja hipotez

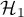By sprawdzić, która z hipotez $\mathcal{H}_0$ czy $\mathcal{H}_1$ jest bardziej prawdopodobna, dobieramy odpowiedni test statystyczny.

Statystyka testowa wybranego testu wyliczana zgodnie z jej wzorem podlega odpowiedniemu dla niej rozkładowi teoretycznemu.

\psset{xunit=1.25cm,yunit=10cm} \begin{pspicture}(-5,-0.1)(5,.5) \psline{->}(-4,0)(4.5,0) \psTDist[linecolor=green,nue=4]{-4}{4} \pscustom[fillstyle=solid,fillcolor=cyan!30]{% \psTDist[linewidth=1pt,nue=4]{-4}{-2.776445}% \psline(-2.776445,0)(-4,0)} \pscustom[fillstyle=solid,fillcolor=cyan!30]{% \psline(2.776445,0)(2.776445,0)% \psTDist[linewidth=1pt,nue=4]{2.776445}{4}% \psline(4,0)(2.776445,0)} \rput(-3.6,0.2){$\alpha/2$} \psline{->}(-3.6,0.15)(-3.1,0.04) \rput(3.6,0.2){$\alpha/2$} \psline{->}(3.6,0.15)(3,0.04) \rput(1,0.5){$1-\alpha$} \psline{->}(1,0.46)(0.55,0.35) \rput(2.5,-0.04){wartość statystyki testowej} \end{pspicture}

Program wylicza wartość statystyki testowej, oraz wartość $p$ dla tej statystyki (czyli część pola pod krzywą, która odpowiada wartości statystyki testowej). Wartość $p$ pozwala wybrać spośród hipotezy zerowej i alternatywnej tę bardziej prawdopodobną. Przy czym zawsze zakładamy prawdziwość hipotezy zerowej, a zebrane w danych dowody mają dostarczyć wystarczającej ilości argumentów przeciwko tej hipotezie:

\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}

Zwykle wybiera się poziom istotności $\alpha=0.05$, zgadzając się, że w 5% sytuacji odrzucimy hipotezę zerową gdy jest ona prawdziwa. W szczególnych przypadkach można wybrać inny poziom istotności np. 0.01 lub 0.001.