Spis treści

Wygładzanie przestrzenne zmiennej

Ideą wygładzania przestrzennego jest uzyskanie zmiennej o lepszych (bardziej stabilnych i odszumionych) wartościach. Najczęściej sposoby budowania takiej zmiennej opierają się na zapożyczeniu informacji z regionów sąsiednich lub wykorzystaniu większej liczby informacji płynącej z regionu badanego (L.A. Waller 2004 1), Luc Anslin 2006 2)).

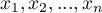W rezultacie wartości badanej zmiennej $X$ o elementach $x_1,x_2,...,x_n$ przekształcone zostaną w nową, wygładzoną zmienną 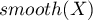$smooth(X)$ o elementach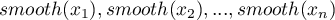 $smooth(x_1),smooth(x_2),...,smooth(x_n)$

 

Wygładzanie lokalne

Badacz ma możliwość sterowania analizą poprzez wybór macierzy odległości/sąsiedztwa obiektów, ustalenie potencjału własnego dla wygładzanego obiektu i wskazanie metody przeprowadzania wygładzania.

Macierz wag przestrzennych

Informacja o sąsiedztwie obiektów i ich wzajemnych odległościach zdefiniowana jest w macierzy wag przestrzennych. Jeśli do wygładzania zostanie wykorzystana macierz sąsiedztwa – niosąca jedynie informację o sąsiadowaniu (1) lub nie (0), wówczas wpływ na uzyskany wynik będą miały tylko obiekty sąsiadujące z badanym i wielkość tego wpływu będzie taka sama dla wszystkich sąsiadów. Gdy badacz chce stopniować wielkość tego wpływu, powinien wybrać macierz o dowolnych wartościach dodatnich. Przy czym należy pamiętać, że większa wartość w macierzy wag daje większy wpływ na wynik wygładzania. Zatem, aby bliższe obiekty miały większy wpływ na uzyskany wynik niż obiekty odległe, powinny posiadać wyższą wagę w macierzy. Taki efekt można osiągnąć stosują na przykład macierz odwrotnej odległości euklidesowej wewnątrz okręgu o promieniu 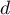$d$. Wówczas obiekty bliższe będą miały większy wpływ na uzyskany wynik niż te odległe, a wpływ obiektów poza okręgiem będzie zerowy. Szerzej metody budowania macierzy wag opisane są w dziale Macierz wag przestrzennych oraz Macierz podobieństwa.

Potencjał własny

Potencjał własny $p$ wygładzanego obiektu decyduje o wielkości wpływu informacji o obiekcie badanym na wygładzoną wartość dla tego obiektu.

Wartość potencjału własnego

Wartość potencjału własnego ustala wielkość elementów umieszczonych na głównej przekątnej macierzy wag. Standardowo wartość potencjału własnego ustawiona jest na 1, podanie wartości zero (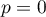$p=0$) powoduje wyliczanie wygładzonej wartości badanego obiektu w oparciu wyłącznie o informacje zawarte w obiektach sąsiednich. Natomiast zwiększanie wartości potencjału własnego zwiększa jego udział w wyliczaniu wygładzonej wartości dla tego obiektu.

Korekcja wartości potencjału

Samo ustawienie wartości potencjału własnego ustala wielkość wpływu badanego obiektu na uzyskany wynik, nie definiuje jednak o ile ten wpływ ma być większy/mniejszy od wpływu obiektów sąsiednich (elementów poza główną przekątną macierzy wag). Uzależnienie wartości na głównej przekątnej macierzy zarówno od podanej wartości potencjału jak i od wartości innych elementów macierzy pozwala na ustalenie wielkości wpływu obiektu badanego w stosunku do obiektów sąsiednich. Korekta wartości potencjału dana jest wzorem:

\begin{displaymath} w_{ii}=p\cdot\sum_{j=1,j\neq i}^n w_{ij} \end{displaymath}

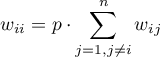
W rezultacie, wybranie opcji korekty wartości potencjału i ustalenie wartości potencjału na przykład na wielkość 3 gwarantuje, że wpływ informacji o obiekcie badanym na wygładzoną wartość dla tego obiektu będzie trzykrotnie wyższy niż obiektów z nim sąsiadujących.

Metody

  • Lokalnie ważona średnia (ang. locally weighted average)

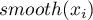Przekształcenie to polega na wyliczeniu średniej arytmetycznej z wartości zmiennej $X$ dla obiektu badanego (wg potencjału) i obiektów z nim sąsiadujących (wg zadanej macierzy wag). Obserwowana wartość $x_i$ przekształcana jest na wygładzoną wartość $smooth(x_i)$ zgodnie z wzorem:

\begin{displaymath} smooth(x_i)=\frac{\sum_{j=1}^n w_{ij}x_j}{\sum_{j=1}^n w_{ij}} \end{displaymath}

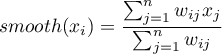
gdzie:

$n$ – liczba obiektów przestrzennych (liczba punktów lub wielokątów),

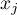$x_j$ – to wartości zmiennej dla porównywanych obiektów,

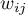$w_{ij}$ – elementy przestrzennej macierzy wag.

  • Lokalnie ważona mediana (ang. locally weighted median)

Przekształcenie to polega na wyliczeniu mediany z wartości zmiennej $X$ dla obiektu badanego (wg potencjału) i obiektów z nim sąsiadujących (wg zadanej macierzy wag). Do jej wyznaczania konieczna jest macierz sąsiedztwa, gdzie wagi są wartościami binarnymi. Wartość jeden w macierzy oznacza sąsiadowanie obiektów a zero brak sąsiedztwa.

  • Lokalnie ważona średnia + dostosowanie (ang. locally weighted average (corrected))

W procesie wygładzania współczynników zbudowanych na bazie dzielenia dwóch zmiennych wyznaczenie lokalnie ważonej średniej można poprawić. Wygładzona jest wówczas dzielna i dzielnik a dopiero na bazie tych wygładzonych wartości tworzony jest iloraz. W ten sposób można na przykład wygładzić współczynniki zachorowania wyznaczane w toku badań epidemiologicznych, gdzie dzielną stanowi liczba chorych a dzielnikiem jest liczność populacji narażonej. W rezultacie obiekty o większej populacji, będą miały większy wpływ na wynik wygładzania - dlatego mianownik wygładzanego współczynnika nazywany jest zmienną dostosowującą.

Obserwowana wartość współczynnika 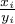$\frac{x_i}{y_i}$ przekształcana jest na wygładzoną wartość 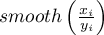$smooth\left(\frac{x_i}{y_i}\right)$ zgodnie z wzorem:

\begin{displaymath} smooth\left(\frac{x_i}{y_i}\right)=\frac{\sum_{j=1}^n w_{ij}x_j}{\sum_{j=1}^n w_{ij}y_j} \end{displaymath}

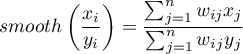
gdzie:

$n$ – liczba obiektów przestrzennych (liczba punktów lub wielokątów),

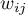$w_{ij}$ – elementy przestrzennej macierzy wag.

  • Empiryczne lokalne wygładzanie Bayes'a + dostosowanie (ang.Empirical Local Bayes Smoothing (corrected))

Metoda lokalnego wygładzania Bayesa została opracowana jako jedna z możliwości radzenia sobie z niestabilnością współczynników związaną z małą licznością danych i została opisana szczegółowo przez Wallera (2004 3)). Wygładzenie ma na celu poprawienie lokalnie ważonej średniej (dostosowanej), tak by ograniczyć jej wariancję.

Obserwowana wartość współczynnika 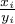$\frac{x_i}{y_i}$ przekształcana jest na wygładzoną wartość 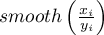$smooth\left(\frac{x_i}{y_i}\right)$ zgodnie z wzorem:

\begin{displaymath} smooth\left(\frac{x_i}{y_i}\right)_{Bayes}=smooth\left(\frac{x_i}{y_i}\right)+C_i\left(\frac{x_i}{y_i}-smooth\left(\frac{x_i}{y_i}\right)\right) \end{displaymath}

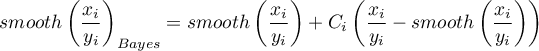
gdzie:

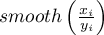$smooth\left(\frac{x_i}{y_i}\right)$- lokalnie ważona średnia (dostosowana)

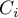$C_i$ – współczynnik kurczenia (ang. shrink factor)

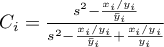$C_i=\frac{s^2-\frac{x_i/y_i}{\bar{y}_i}}{s^2-\frac{x_i/y_i}{\bar{y}_i}+\frac{x_i/y_i}{y_i}}$ jeśli $s^2-\frac{x_i/y_i}{\bar{y}_i}>0$

$s_i^2=\frac{\sum_{j=1}^ne_{ij}}{\sum_{j=1}^ny_jw_{ij}}$

$e_{ij}=y_i\left(\frac{x_i}{y_i}w_{ij}-smooth\left(\frac{x_i}{y_i}\right)\right)$

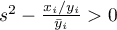
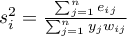
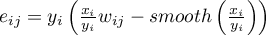
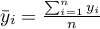$\bar{y}_i=\frac{\sum_{i=1}^ny_i}{n}$ – to średnia liczność populacji,

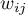$w_{ij}$ – elementy przestrzennej macierzy wag.

Współczynnik kurczenia pozwala balansować pomiędzy lokalną średnią 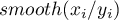$smooth(x_i/y_i)$ a obserwowaną wartością współczynnika 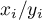$x_i/y_i$. Kiedy liczność zmiennej dostosowującej 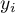$y_i$ (liczność populacji) jest mała, wówczas 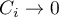$C_i\to 0$ i estymowana wartość jest bliska lokalnie ważonej średniej dostosowanej 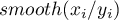$smooth(x_i/y_i)$ . 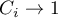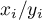Gdy liczność populacji jest duża, wówczas $C_i\to 1$ i estymowana wartość zbliża się do rzeczywistej wartości obserwowanej w tym obiekcie $x_i/y_i$.

2015/12/28 13:16 · admin
1) , 3)
Waller L.A., Gotway C.A. (2004), Applied Spatial Statistics for Public Health Data. New York: John Wiley and Sons
2)
Anselin L., Lozano N., Koschinsky J. (2006) Rate Transformations and Smoothing. GeoDa Center Research Report, https://geodacenter.asu.edu