Analiza losowości rozkładu punktów
By przeprowadzić analizę losowości rozkładu punktów powinniśmy dysponować danymi mapy zawierającej obiekty typu: punkt, wielopunkt lub wielokąt. W przypadku analizy wielokątów obliczenia oparte są na centroidach, a przypadku wielopunktów na centrach obiektów.
Efekt równomiernego rozproszenia występuje wówczas, gdy punkty są rozłożone bardziej regularnie niż mogłoby to wynikać z rozkładu losowego. Jeśli uzyskany rozkład przestrzenny jest tak samo prawdopodobny jak w każdy inny rozkład - mówimy wówczas o przestrzennej losowości. Gdy punkty grupują się, to możemy mówić o występowaniu rozkładu skupiskowego.
![LaTeX \begin{pspicture}(1,-1)(12.5,4.5)
\psline{-}(5,0)(5,4)
\psline{-}(5,0)(9,0)
\psline{-}(5,4)(9,4)
\psline{-}(9,0)(9,4)
\rput(7.12,1.31){$\circ$}
\rput(5.63,3.33){$\circ$}
\rput(6.56,3.86){$\circ$}
\rput(8.18,0.04){$\circ$}
\rput(5.08,0.91){$\circ$}
\rput(8.4,2.98){$\circ$}
\rput(5.03,3.61){$\circ$}
\rput(7.46,3.33){$\circ$}
\rput(6.7,1.23){$\circ$}
\rput(8.43,3.06){$\circ$}
\rput(7.66,3.75){$\circ$}
\rput(5.82,1.7){$\circ$}
\rput(5.01,2.85){$\circ$}
\rput(7.4,0.67){$\circ$}
\rput(6.68,2.48){$\circ$}
\rput(7.42,2.03){$\circ$}
\rput(8.3,0.93){$\circ$}
\rput(8.82,2.14){$\circ$}
\rput(6.62,3.86){$\circ$}
\rput(6.73,1.99){$\circ$}
\rput(5.9,2.11){$\circ$}
\rput(7.73,1.51){$\circ$}
\rput(7.53,0.08){$\circ$}
\rput(5.72,1.52){$\circ$}
\rput(8.92,3.77){$\circ$}
\psline{-}(0,0)(0,4)
\psline{-}(0,0)(4,0)
\psline{-}(0,4)(4,4)
\psline{-}(4,0)(4,4)
\rput(0,0){$\circ$}
\rput(0,1){$\circ$}
\rput(0,2){$\circ$}
\rput(0,3){$\circ$}
\rput(0,4){$\circ$}
\rput(1,0){$\circ$}
\rput(1,1){$\circ$}
\rput(1,2){$\circ$}
\rput(1,3){$\circ$}
\rput(1,4){$\circ$}
\rput(2,0){$\circ$}
\rput(2,1){$\circ$}
\rput(2,2){$\circ$}
\rput(2,3){$\circ$}
\rput(2,4){$\circ$}
\rput(3,0){$\circ$}
\rput(3,1){$\circ$}
\rput(3,2){$\circ$}
\rput(3,3){$\circ$}
\rput(3,4){$\circ$}
\rput(4,0){$\circ$}
\rput(4,1){$\circ$}
\rput(4,2){$\circ$}
\rput(4,3){$\circ$}
\rput(4,4){$\circ$}
\psline{-}(10,0)(10,4)
\psline{-}(10,0)(14,0)
\psline{-}(10,4)(14,4)
\psline{-}(14,0)(14,4)
\rput(10.79,0.61){$\circ$}
\rput(11.21,0.84){$\circ$}
\rput(11.32,1.11){$\circ$}
\rput(11.37,0.58){$\circ$}
\rput(10.7,0.34){$\circ$}
\rput(10.43,0.58){$\circ$}
\rput(10.58,0.17){$\circ$}
\rput(10.62,0.41){$\circ$}
\rput(11.61,0.31){$\circ$}
\rput(10.47,0.84){$\circ$}
\rput(12.93,3.06){$\circ$}
\rput(13.23,3.69){$\circ$}
\rput(12.59,2.84){$\circ$}
\rput(13.42,3.27){$\circ$}
\rput(13.67,2.91){$\circ$}
\rput(13.08,2.94){$\circ$}
\rput(13.4,3.33){$\circ$}
\rput(13.3,3.68){$\circ$}
\rput(12.66,3.3){$\circ$}
\rput(10.98,3.66){$\circ$}
\rput(11.31,3.45){$\circ$}
\rput(11.43,3.36){$\circ$}
\rput(13.54,0.4){$\circ$}
\rput(13.86,0.38){$\circ$}
\rput(13.31,0.53){$\circ$}
\psline[linewidth=3pt]{<->}(0,-0.5)(14,-0.5)
\rput(1.5,-1){rozkład równomierny}
\rput(7,-1){rozkład losowy}
\rput(13,-1){rozkład skupiskowy}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img3766ba8e5fda9a804864b6c4121aed4e.png)
Analiza najbliższego sąsiedztwa
W Analizie najbliższego sąsiedztwa (ang. Nearest Neighbor Analysis) granice obszaru, w którym zamknięte są analizowane punkty, mają zasadniczy wpływ na uzyskany wynik. Poniższy przykład daje obraz regularnie rozłożonych punktów, gdy ich granicą jest mały prostokąt i rozkładu skupiskowego, gdy ich granicą jest duży prostokąt.
(5,2.5)
\psline[linestyle=dashed](5,0)(8,0)
\psline[linestyle=dashed](5,2.5)(8,2.5)
\psline[linestyle=dashed](8,0)(8,2.5)
\psline{-}(5.7,0.5)(5.7,2)
\psline{-}(5.7,0.5)(7.3,0.5)
\psline{-}(5.7,2)(7.3,2)
\psline{-}(7.3,0.5)(7.3,2)
\rput(6.2,1){$\circ$}
\rput(6.8,1.5){$\circ$}
\rput(6.2,1.5){$\circ$}
\rput(6.8,1){$\circ$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgaeab4b2d3483753a4db8950ca4951980.png)
Granice, w zależności od potrzeb, mogą być zdefiniowane za pomocą: otoczki wypukłej, najmniejszego prostokąta, prostokąta z granic warstwy lub najmniejszego okręgu. Badany obszar może być również zdefiniowany jedynie przez wielkość swojego pola.
Odległość pomiędzy punktami mierzona jest metryką Euklidesową.
Pierwszym etapem analizy najbliższego sąsiedztwa jest wyliczenie odległości pomiędzy wszystkimi punktami. Następnie dla każdego punktu szukany jest punkt, który jest położony najbliżej tzw. najbliższe sąsiedztwo (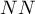 ).
).
Uwaga!
Odległości pomiędzy wszystkimi punktami definiowane są poprzez macierz wag. W oknie analizy najbliższego sąsiedztwa możemy wybrać macierz wag wygenerowaną wcześniej za pomocą menu Analiza przestrzenna → Narzędzia → Macierz wag przestrzennych lub wskazać proponowaną przez program macierz wszystkich odległości wyliczanych zgodnie z metryką Euklidesową.
Podstawowe statystyki dla analizy najbliższych sąsiadów:
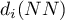 - odległość każdego punktu od jego najbliższego sąsiada,
- odległość każdego punktu od jego najbliższego sąsiada,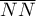 - średnia odległość najbliższych sąsiadów:
- średnia odległość najbliższych sąsiadów:
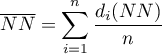
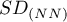 - odchylenie standardowe odległości najbliższych sąsiadów,
- odchylenie standardowe odległości najbliższych sąsiadów,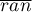 - średnia oczekiwana odległość najbliższych sąsiadów:
- średnia oczekiwana odległość najbliższych sąsiadów:
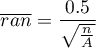
Współczynnik Najbliższego Sąsiedztwa
Współczynnik Najbliższego Sąsiedztwa (ang. Nearest Neighbor Index (NNI)) bazuje na metodzie opisanej przez botaników: Clarka i Evansa (1954)1). 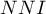 porównuje obserwowane odległości pomiędzy najbliższymi punktami oraz odległości, które pojawiłyby się dla losowego rozkładu punktów.
porównuje obserwowane odległości pomiędzy najbliższymi punktami oraz odległości, które pojawiłyby się dla losowego rozkładu punktów.
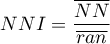 Kiedy porównywane odległości są takie same, wówczas
Kiedy porównywane odległości są takie same, wówczas 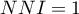 . Kiedy obserwowane odległości pomiędzy najbliższymi punktami są mniejsze niż oczekiwane, wówczas punkty są bliżej siebie niż w rozkładzie losowym i
. Kiedy obserwowane odległości pomiędzy najbliższymi punktami są mniejsze niż oczekiwane, wówczas punkty są bliżej siebie niż w rozkładzie losowym i 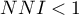 . Tworzą się skupiska. Gdy jest odwrotnie, wówczas
. Tworzą się skupiska. Gdy jest odwrotnie, wówczas 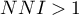 , co świadczy o występowaniu efektu równomiernego rozproszenia, czyli punkty są regularniej umiejscowione niż wynikałoby to z ich losowego rozkładu.
, co świadczy o występowaniu efektu równomiernego rozproszenia, czyli punkty są regularniej umiejscowione niż wynikałoby to z ich losowego rozkładu.
Istotności Współczynnika Najbliższego Sąsiedztwa
Test do sprawdzania istotności Współczynnika Najbliższego Sąsiedztwa 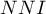 służy do weryfikacji hipotezy o tym, że obserwowane odległości pomiędzy najbliższymi punktami są takie same jak oczekiwane odległości, które pojawiłyby się dla losowego rozkładu punktów.
służy do weryfikacji hipotezy o tym, że obserwowane odległości pomiędzy najbliższymi punktami są takie same jak oczekiwane odległości, które pojawiłyby się dla losowego rozkładu punktów.
Hipotezy:
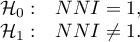
Statystyka testowa ma postać:
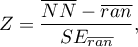
gdzie:
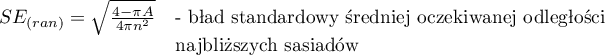
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wartość  , wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności
, wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności  :
:

Analiza kolejnych najbliższych sąsiadów
By analizować kolejnych najbliższych sąsiadów, bierze się pod uwagę odległość do drugiego najbliższego sąsiada, trzeciego najbliższego sąsiada, aż do  -tego najbliższego sąsiada. Dla sąsiedztwa każdego stopnia (od najbliższego sąsiedztwa do sąsiedztwa
-tego najbliższego sąsiada. Dla sąsiedztwa każdego stopnia (od najbliższego sąsiedztwa do sąsiedztwa  -tego stopnia) wylicza się kolejne Współczynniki Najbliższego Sąsiedztwa:
-tego stopnia) wylicza się kolejne Współczynniki Najbliższego Sąsiedztwa:
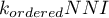 :
:
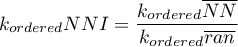
gdzie:
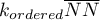 - średnia odległość do sąsiadów
- średnia odległość do sąsiadów  -tego stopnia,
-tego stopnia,
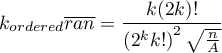 - średnia oczekiwana odległość do sąsiadów
- średnia oczekiwana odległość do sąsiadów  -tego stopnia.
-tego stopnia.
Wyniki analizy gęstości punktów przeprowadzanej dla kolejnych sąsiadów można przedstawić na wykresie, aby zobrazować w ten sposób położenie współczynników 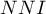 w stosunku do linii wskazującej losową strukturę punktów oraz by sprawdzić, czy dla współczynników uzyskano trend rosnący lub malejący.
w stosunku do linii wskazującej losową strukturę punktów oraz by sprawdzić, czy dla współczynników uzyskano trend rosnący lub malejący.
Efekt krawędzi
Obiekty znajdujące się blisko granicy wykazują tendencję do większego oddalenia od najbliższych sąsiadów, niż inne obiekty znajdujące się w obszarze analizy. Wynika to z prostego faktu, że najbliżsi sąsiedzi obiektów przygranicznych mogą znajdować się poza granicami badanego obszaru. W takiej sytuacji można przeprowadzić analizę z korektą efektu granicy.
Wówczas odległość punktu od jego najbliższego sąsiada (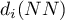 ) jest wyliczana jako minimum odległości punktu od jego sąsiadów i od granicy. Jeśli więc odległość punktu od granicy będzie mniejsza niż do jego sąsiadów, wówczas za
) jest wyliczana jako minimum odległości punktu od jego sąsiadów i od granicy. Jeśli więc odległość punktu od granicy będzie mniejsza niż do jego sąsiadów, wówczas za 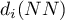 przyjmowana jest odległość do granicy. Jednakże takie wyliczenie najbliższego sąsiedztwa wymaga założenia, że na granicy zawsze znajduje się punkt uznawany za sąsiada.
przyjmowana jest odległość do granicy. Jednakże takie wyliczenie najbliższego sąsiedztwa wymaga założenia, że na granicy zawsze znajduje się punkt uznawany za sąsiada.
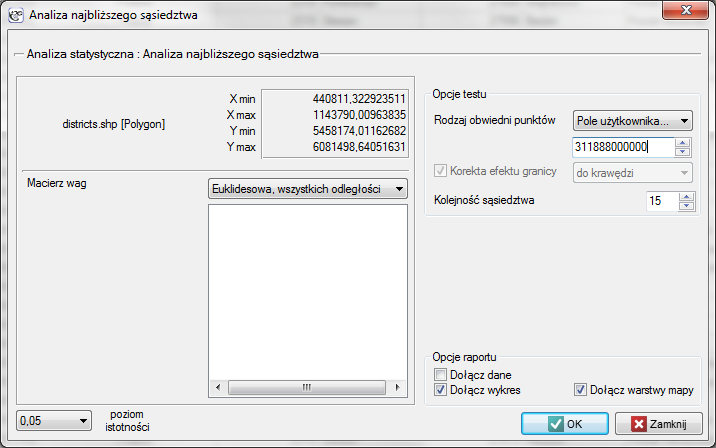
Okno z ustawieniami opcji analizy najbliższego sąsiedztwa wywołujemy poprzez menu Analiza przestrzenna→Statystyki przestrzenne→Analiza najbliższego sąsiedztwa.
Przykład (katalog: districts, pliki SHP: districts)
Podział administracyjny Polski na powiaty z założenia powinien być równomierny. Czy tak rzeczywiście jest, sprawdzimy przy użyciu współczynnika NNI.
- Mapa
districtszawiera informacje o lokalizacji wielokątów (powiatów Polski).
Analiza najbliższego sąsiedztwa będzie się opierać na centroidach reprezentujących powiaty. Możemy je wyrysować (dodać warstwę centroid do mapy powiatów) korzystając z Menadżera map.
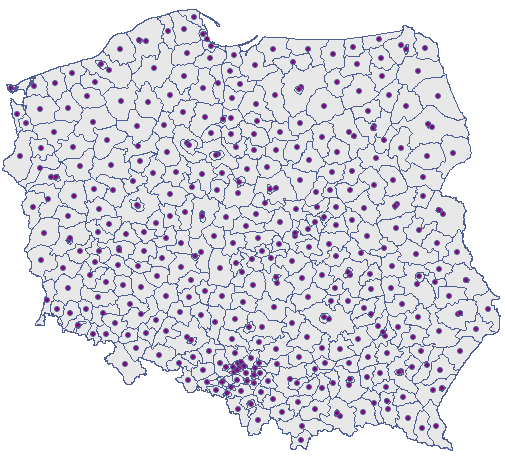
Analizę najbliższego sąsiedztwa przeprowadzimy wykorzystując informację o wielkości pola powierzchni Polski - wynosi ono 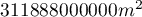 . Oprócz współczynnika pierwszego sąsiedztwa wyliczymy też współczynniki kolejnego sąsiedztwa aż do 15.
. Oprócz współczynnika pierwszego sąsiedztwa wyliczymy też współczynniki kolejnego sąsiedztwa aż do 15.
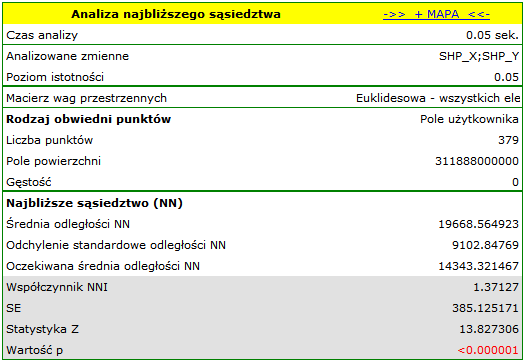
Podając wielkość pola w oknie analizy, uzyskano współczynnik najbliższego sąsiedztwa równy 1.37127 i istotnie statystycznie większy od wartości 1 (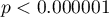 ). Średnia odległość pomiędzy najbliższymi sąsiednimi centroidami wynosi
). Średnia odległość pomiędzy najbliższymi sąsiednimi centroidami wynosi 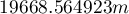 a odchylenie standardowe to
a odchylenie standardowe to 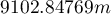 . Bardzo podobny rezultat uzyskamy, gdy powrócimy do analizy (przycisk
. Bardzo podobny rezultat uzyskamy, gdy powrócimy do analizy (przycisk  ) i jako obwiednię obiektów wybierzemy otoczkę wypukłą (
) i jako obwiednię obiektów wybierzemy otoczkę wypukłą (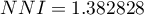 ,
, 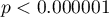 ).
).
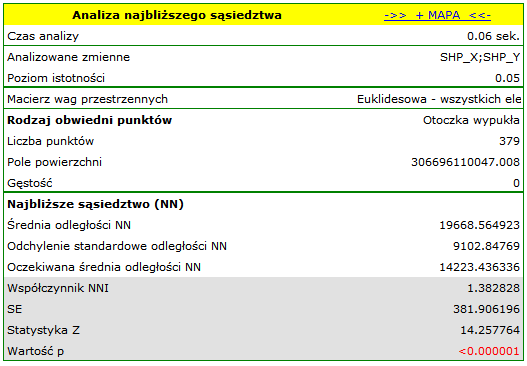
Granice wyznaczone przez otoczkę wypukłą dodajemy do mapy uruchamiając przycisk  i wybierając warstwę obwiedni obiektów.
i wybierając warstwę obwiedni obiektów.
Zastosowanie korekty efektu tak rozumianej granicy obniża wartość 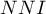 do 1.340503 ale pozostawia niezmienioną ogólną tendencję kolejnych współczynników najbliższego sąsiedztwa.
do 1.340503 ale pozostawia niezmienioną ogólną tendencję kolejnych współczynników najbliższego sąsiedztwa.
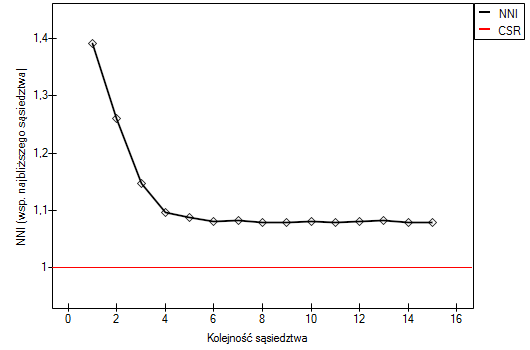
W każdej z powyższych analiz kolejne współczynniki sąsiedztwa są większe niż 1 i mimo, że początkowo zbliżają się do 1, to od stopnia 5 stabilizują się na poziomie ok 1.1. Uzyskany wynik potwierdza zatem równomierne rozłożenie powiatów w Polsce.
Przykład (katalog: poplar, pliki SHP: T-poplar, S-poplar)
Konkurencja międzygatunkowa wpływa na zmiany w rozmieszczeniu poszczególnych gatunków roślin i ich zagęszczeniu. Konkurencja wewnątrzgatunkowa jest zwykle silniejsza od konkurencji międzygatunkowej, gdyż osobniki tego samego gatunku mają niemal identyczne wymagania i współzawodniczą o te same zasoby. Natężenie konkurencji wewnątrzgatunkowej rośnie wraz ze wzrostem liczebności populacji. By sprawdzić wpływ konkurencji na pewien gatunek topoli balsamicznej, analizie poddano obszar leśny nie regulowany przez człowieka. Badano lokalizację drzew młodych i drzew dorosłych.
- Mapa
T-poplarzawiera fikcyjne informacje o lokalizacji 121 punktów (dużych topoli balsamicznych) w prostokątnym wycinku lasu. - Mapa
S-poplarzawiera fikcyjne informacje o lokalizacji 326 punktów (małych topoli balsamicznych) w prostokątnym wycinku lasu.
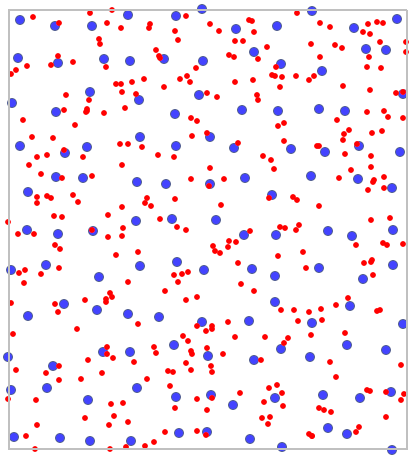
Na mapie drzewa młode (małe) oznaczono kolorem czerwonym a drzewa dorosłe (duże) kolorem niebieskim.
Na podstawie współczynników najbliższego sąsiedztwa, w obszarze wyznaczonym przez prostokąt z granic warstwy, porównana została struktura zagęszczenia topoli.
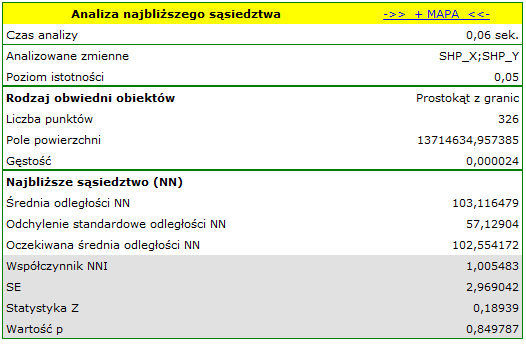
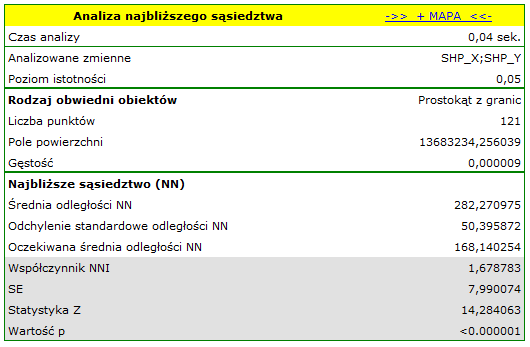
Drzewa młode występują gęściej niż drzewa dorosłe. Ich średnia odległość najbliższych sąsiadów wynosi 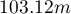 , podczas gdy dla drzew dorosłych
, podczas gdy dla drzew dorosłych 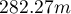 .
Konkurencja w rozwoju struktury drzewostanu sprawia, że przestrzenny wzór dużych drzew jest bardziej regularny (
.
Konkurencja w rozwoju struktury drzewostanu sprawia, że przestrzenny wzór dużych drzew jest bardziej regularny (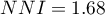 ,
, 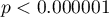 ) niż w przypadku drzew małych (
) niż w przypadku drzew małych (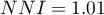 ,
, 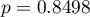 ).
).