Spis treści
Rozkłady prawdopodobieństwa
Rzeczywisty rozkład danych z próby - rozkład empiryczny danych może być przedstawiony za pomocą Tabel liczności (poprzez wybranie menu Statystyka→Analizy opisowe→Tabele liczności). Na przykład rozkład ilości wykorzystanych darmowych minut przez abonentów pewnego operatora telefonii komórkowej.
Przykład (plik: rozkład.pqs) przedstawia następująca tabela:
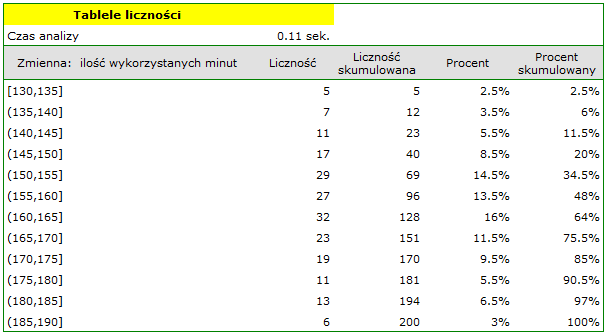
Graficzna prezentacja wyników uzyskanych w raporcie tabeli zwykle dokonywana jest przy pomocy histogramu czy też wykresu kolumnowego.
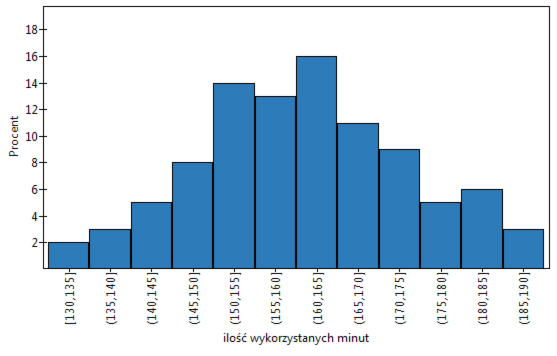
Wykres taki możemy uzyskać zaznaczając w oknie Tabel licznosci opcje Dołącz wykres.
Rozkład teoretyczny danych zwany również rozkładem prawdopodobieństwa graficznie przedstawiany jest zwykle przy pomocy wykresu liniowego. Taka linia opisana jest funkcją (modelem matematycznym) i zwana funkcją gęstości rozkładu. Odpowiednim rozkładem teoretycznym można zastąpić rozkład empiryczny.
Uwaga! Do zastąpienia rozkładu empirycznego rozkładem teoretycznym nie wystarczy intuicyjne stwierdzenie podobieństwa ich przebiegu. Służą do tego specjalnie skonstruowane testy zgodności z tym rozkładem.
Najczęściej używanym rozkładem prawdopodobieństwa jest rozkład normalny (rozkład Gaussa), i taki rozkład o średniej 161.15 i odchyleniu standardowym równym 13.03 prezentują dane na temat ilości wykorzystanych darmowych minut (Przykład plik: rozkład.pqs). 1
Ciągłe rozkłady prawdopodobieństwa
Funkcja gęstości jest zdefiniowana jako:
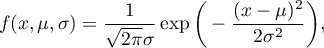
gdzie:
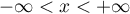 ,
,
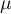
 wartość oczekiwana populacji (której miarą jest średnia),
wartość oczekiwana populacji (której miarą jest średnia),
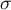
 odchylenie standardowe.
odchylenie standardowe.
![LaTeX \psset{xunit=1.25cm,yunit=8cm}
\begin{pspicture}(-3.5,-.1)(4.2,0.9)
\psaxes[Dy=0.1]{->}(0,0)(-4.5,0)(5,0.9)
\uput[-90](5,0){x}\uput[0](0,0.85){y}
\psGauss[linecolor=red, linewidth=2pt, mue=0, sigma=1]{-4}{4}%
\rput(1.5,0.27){\textcolor{red}{$N(0,1)$}}
\psGauss[linecolor=blue, linestyle=dotted, mue=1, sigma=1]{-4}{4}%
\rput(2.6,0.25){\textcolor{blue}{$N(1,1)$}}
\psGauss[linecolor=green,linestyle=dashed, mue=0, sigma=0.5]{-4}{4}%
\rput(1.1,0.6){\textcolor{green}{$N(0,4)$}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgdf0de30603271e67b32774a2ab3da458.png)
Rozkład normalny jest rozkładem symetrycznym względem prostej prostopadłej do osi odciętych i przechodzącej przez punkt wyznaczający średnią, modę oraz medianę.
Rozkład normalny o średniej 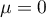 i
i  (
(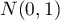 ), to tzw. rozkład normalny standaryzowany.
), to tzw. rozkład normalny standaryzowany.
Funkcja gęstości jest zdefiniowana jako:
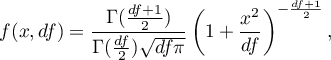
gdzie:
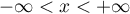 ,
,
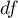
 stopnie swobody (liczność próby pomniejszona o liczbę ograniczeń w określonych obliczeniach),
stopnie swobody (liczność próby pomniejszona o liczbę ograniczeń w określonych obliczeniach),
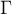 to funkcja Gamma.
to funkcja Gamma.
![LaTeX \psset{xunit=1.25cm,yunit=10cm}
\begin{pspicture}(-5,-0.1)(5,.5)
\psaxes[Dy=0.1]{->}(0,0)(-4.5,0)(5,0.5)
\uput[-90](5,0){x}\uput[0](0,0.45){y}
\psGauss[linecolor=red, linewidth=2pt, mue=0, sigma=1]{-4}{4}%
\rput(1.6,0.25){\textcolor{red}{$N(0,1)$}}
\psTDist[linecolor=blue,linestyle=dotted,nue=1]{-4}{4}
\rput(2.5,0.2){\textcolor{blue}{$T(df=1)$}}
\psTDist[linecolor=green,linestyle=dashed,nue=4]{-4}{4}
\rput(3,0.15){\textcolor{green}{$T(df=4)$}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img87732e4f73e787194a3883f4b421d9a0.png)
Funkcja gęstości jest zdefiniowana jako:
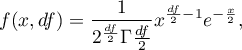
gdzie:
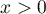 ,
,
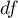
 stopnie swobody (liczność próby pomniejszona o liczbę ograniczeń w określonych obliczeniach),
stopnie swobody (liczność próby pomniejszona o liczbę ograniczeń w określonych obliczeniach),
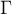 to funkcja Gamma.
to funkcja Gamma.
{x}\uput[0](0,0.55){y}
\psChiIIDist[linewidth=1pt,linecolor=red, nue=1,]{0.01}{9}
\rput(1.8,0.4){\textcolor{red}{$\chi^2(df=1)$}}
\psChiIIDist[linewidth=1pt,linecolor=blue,linestyle=dotted, nue=5,]{0.01}{9}
\rput(4,0.2){\textcolor{blue}{$\chi^2(df=5)$}}
\psChiIIDist[linewidth=1pt,linecolor=green,linestyle=dashed, nue=10,]{0.01}{9}
\rput(8,0.15){\textcolor{green}{$\chi^2(df=10)$}}
\psaxes[Dy=0.1]{->}(0,0)(9.5,.6)
\end{pspicture*}](/lib/exe/fetch.php?media=wiki:latex:/img223648a7521a83822018c081beb401d1.png)
Funkcja gęstości jest zdefiniowana jako:
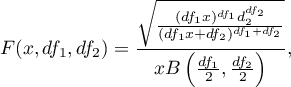
gdzie:
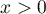 ,
,
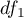 ,
, 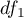
 stopnie swobody (przyjmuje się, że jeżeli
stopnie swobody (przyjmuje się, że jeżeli  i
i  są niezależne o rozkładzie
są niezależne o rozkładzie  z odpowiednio
z odpowiednio 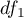 i
i 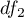 stopniami swobody, to
stopniami swobody, to 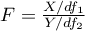 ma rozkład F Snedecora
ma rozkład F Snedecora 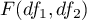 ),
),
 to funkcja Beta.
to funkcja Beta.
![LaTeX \psset{xunit=2cm,yunit=10cm,plotpoints=100}
\begin{pspicture*}(-0.5,-0.07)(5.5,0.8)
\psFDist[linecolor=green,linestyle=dashed]{0.1}{5}
\rput(1,0.05){\textcolor{green}{$F(df_1=1,df_2=1)$}}
\psFDist[linecolor=red,nue=3,mue=12]{0.01}{5}
\rput(4,0.15){\textcolor{red}{$F(df_1=3,df_2=12)$}}
\psFDist[linecolor=blue,linestyle=dotted,nue=12,mue=3]{0.01}{5}
\rput(2,0.4){\textcolor{blue}{$F(df_1=12,df_2=3)$}}
\psaxes[Dy=0.1]{->}(0,0)(5,0.75)
\end{pspicture*}](/lib/exe/fetch.php?media=wiki:latex:/img4153af385b1104035518012189a91db9.png)
Kalkulator funkcji dystrybucji
Pole pod krzywą (funkcją gęstości rozkładu) to prawdopodobieństwo  wystąpienia wszystkich możliwych wartości badanej zmiennej losowej. Całe pole pod krzywą wynosi
wystąpienia wszystkich możliwych wartości badanej zmiennej losowej. Całe pole pod krzywą wynosi 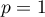 . Gdy chcemy zbadać wielkość tylko części tego pola musimy podać wartość graniczną zwaną wartością krytyczną lub
. Gdy chcemy zbadać wielkość tylko części tego pola musimy podać wartość graniczną zwaną wartością krytyczną lub Statystyką. Korzystamy w tym celu z okna Kalkulatora funkcji dystrybucji. W oknie tym jest możliwe wyliczanie wartości pola pod krzywą (Wartość  ) zadanego rozkładu na podstawie
) zadanego rozkładu na podstawie Statystyki, jak też wyznaczanie wartości Statystyki na podstawie Wartości . Okno
. Okno Kalkulatora funkcji dystrybucji uruchamiamy poprzez wybranie menu Statystyka→Kalkulatory→Kalkulator funkcji dystrybucji
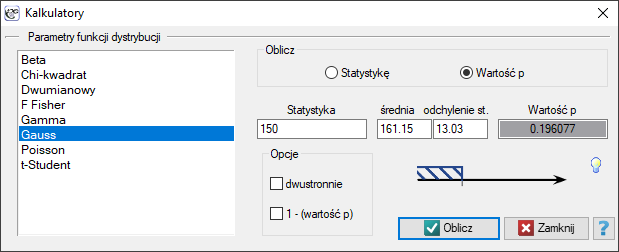
Kalkulator funkcji dystrybucji
Pewien operator telefonii komórkowej przeprowadza szereg badań dotyczących wykorzystania przez klientów ilości przyznanych w abonamencie „darmowych minut”. Na podstawie 200 osobowej próby swoich klientów (w której rozkład wykorzystanych „darmowych minut” przyjmuje kształt rozkładu normalnego) wyznaczył wartość średnią 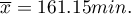 i odchylenie standardowe
i odchylenie standardowe 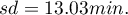 Chcemy wyliczyć prawdopodobieństwo, że wylosowany przez nas klient wykorzystał:
Chcemy wyliczyć prawdopodobieństwo, że wylosowany przez nas klient wykorzystał:
- 150 minut lub mniej,
- więcej niż 150 minut,
- ilość minut z przedziału
![LaTeX $[\overline{x}- sd,\overline{x}+ sd] =[148.12min.,174.18min.]$](/lib/exe/fetch.php?media=wiki:latex:/imge95ee390798d5f324a87a7ff392a75a6.png) ,
, - ilość minut spoza przedziału
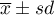 .
.
Uruchamiamy okno Kalkulatora funkcji dystrybucji, wybieramy rozkład Gaussa i wpisujemy średnią 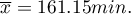 i
i odchylenie st. 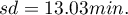 oraz zaznaczamy, że będziemy wyliczać
oraz zaznaczamy, że będziemy wyliczać Wartość  .
.
- By wyliczyć na podstawie rozkładu normalnego (Gaussa) jakie jest prawdopodobieństwo, że klient którego wylosujemy wykorzystał 150 darmowych minut lub mniej, w polu
Statystykawpisujemy wartość 150. Wybrane ustawienia potwierdzamy przyciskiemOblicz.
![LaTeX \psset{xunit=1.2cm,yunit=8cm}
\begin{pspicture}(-3.5,-.05)(4.2,0.4)
\psline{-}(-4,0)(4,0)
\psGauss[linecolor=blue, mue=0, sigma=1]{-4}{4}%
\pscustom[fillstyle=solid,fillcolor=red!30]{%
\psGauss[linewidth=1pt,mue=0, sigma=1]{-4}{-0.85572}%
\psline(-0.85572,0)(-4,0)}
\rput(2.4,0.25){\textcolor{blue}{$N(161.15,13.03)$}}
\rput(-0.85572,-0.05){\textcolor{blue}{150}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img3c7c1127f8168931642e12a3d7aae440.png)
UzyskanaWartość wynosi 0.193961.
wynosi 0.193961.
Uwaga!
Podobne obliczenia możemy wykonać na podstawie rozkładu empirycznego. Wystarczy wówczas przy pomocy oknaTabele licznościwyznaczyć procent klientów wykorzystujących 150 minut lub mniej (patrz przykład (\ref{tab_licznosci}), plik: rozkład.pqs). W badanej 200 osobowej próbie klientów wykorzystujących 150 minut lub mniej jest 40, co stanowi 20\% próby a zatem szukane prawdopodobieństwo wynosi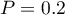 .
.
- By wyliczyć na podstawie rozkładu normalnego (Gaussa) jakie jest prawdopodobieństwo, że klient którego wylosujemy wykorzystał więcej niż 150 darmowych minut, w polu
Statystykawpisujemy wartość 150 i zaznaczamy opcję1- Wartość . Wybrane ustawienia potwierdzamy przyciskiem
. Wybrane ustawienia potwierdzamy przyciskiem Oblicz.
![LaTeX \psset{xunit=1.2cm,yunit=8cm}
\begin{pspicture}(-3.5,-.05)(4.2,0.4)
\psline{-}(-4,0)(4,0)
\psGauss[linecolor=blue, mue=0, sigma=1]{-4}{4}%
\pscustom[fillstyle=solid,fillcolor=red!30]{%
\psline(-0.85572,0)(-0.85572,0)%
\psGauss[linewidth=1pt,mue=0, sigma=1]{-0.85572}{4}%
\psline(4,0)(-0.85572,0)}
\rput(2.4,0.25){\textcolor{blue}{$N(161.15,13.03)$}}
\rput(-0.85572,-0.05){\textcolor{blue}{150}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img880f38e5b626288ec2683062b11adc2f.png)
UzyskanaWartość wynosi 0.806039.
wynosi 0.806039.
- By wyliczyć na podstawie rozkładu normalnego (Gaussa) jakie jest prawdopodobieństwo, że klient którego wylosujemy wykorzystał minuty z przedziału
![LaTeX $[\overline{x}- sd,\overline{x}+ sd] =[148.12min.,174.18min.]$](/lib/exe/fetch.php?media=wiki:latex:/imge95ee390798d5f324a87a7ff392a75a6.png) , w polu
, w polu Statystykawpisujemy jedną z końcowych wartości przedziału, a następnie zaznaczamy opcjędwustronnie. Wybrane ustawienia potwierdzamy przyciskiemOblicz.
![LaTeX \psset{xunit=1.2cm,yunit=8cm}
\begin{pspicture}(-3.5,-.05)(4.2,0.4)
\psline{-}(-4,0)(4,0)
\psGauss[linecolor=blue, mue=0, sigma=1]{-4}{4}%
\pscustom[fillstyle=solid,fillcolor=red!30]{%
\psline(-1,0)(-1,0)%
\psGauss[linewidth=1pt,mue=0, sigma=1]{-1}{1}%
\psline(1,0)(-1,0)}
\rput(2.4,0.25){\textcolor{blue}{$N(161.15,13.03)$}}
\rput(-1,-0.05){\textcolor{blue}{148.12}}
\rput(1,-0.05){\textcolor{blue}{174.18}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgc26fc1da363b6ae663ba5efe85065299.png)
UzyskanaWartość wynosi 0.682689.
wynosi 0.682689.
- By wyliczyć na podstawie rozkładu normalnego (Gaussa) jakie jest prawdopodobieństwo, że klient którego wylosujemy wykorzystał minuty spoza przedziału
![LaTeX $[\overline{x}- sd,\overline{x}+ sd] =[148.12min.,174.18min.]$](/lib/exe/fetch.php?media=wiki:latex:/imge95ee390798d5f324a87a7ff392a75a6.png) , w polu
, w polu Statystykawpisujemy jedną z końcowych wartości przedziału, a następnie zaznaczamy opcje:dwustronniei1-wartość . Wybrane ustawienia potwierdzamy przyciskiem
. Wybrane ustawienia potwierdzamy przyciskiem Oblicz.
![LaTeX \psset{xunit=1.2cm,yunit=8cm}
\begin{pspicture}(-3.5,-.05)(4.2,0.4)
\psline{-}(-4,0)(4,0)
\psGauss[linecolor=blue, mue=0, sigma=1]{-4}{4}%
\pscustom[fillstyle=solid,fillcolor=red!30]{%
\psGauss[linewidth=1pt,mue=0, sigma=1]{-4}{-1}%
\psline(-1,0)(-4,0)}
\pscustom[fillstyle=solid,fillcolor=red!30]{%
\psline(1,0)(1,0)%
\psGauss[linewidth=1pt,mue=0, sigma=1]{1}{4}%
\psline(4,0)(1,0)}
\rput(2.4,0.25){\textcolor{blue}{$N(161.15,13.03)$}}\rput(-1,-0.05){\textcolor{blue}{148.12}}
\rput(1,-0.05){\textcolor{blue}{174.18}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img65581d342db71d064052a88b203192c0.png)
UzyskanaWartość wynosi 0.317311.
wynosi 0.317311.
Proces uogólnienia wyników otrzymanych dla próby na całą populację dzieli się zasadniczo na 2 części:
- estymację
 szacowanie wartości parametrów populacji na podstawie próby statystycznej,
szacowanie wartości parametrów populacji na podstawie próby statystycznej, - weryfikację hipotez statystycznych
 sprawdzanie określonych założeń sformułowanych dla parametrów populacji generalnej na podstawie wyników z próby.
sprawdzanie określonych założeń sformułowanych dla parametrów populacji generalnej na podstawie wyników z próby.
 .
.