Analysis of model residuals

To obtain a correct regression model we should check the basic assumptions concerning model residuals.

The study of the model residual can be a quick source of knowledge about outlier values. Such observations can disturb the equation of the regression to a large extent because they have a great effect on the values of the coefficients in the equation. If the given residual 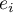$e_i$ deviates by more than 3 standard deviations from the mean value, such an observation can be classified as an outlier. A removal of an outlier can greatly enhance the model.

Cook's distance - describes the magnitude of change in regression coefficients produced by omitting a case. In the program, Cook's distances for cases that exceed the 50th percentile of the F-Snedecor distribution statistic are highlighted in bold 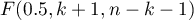$F(0.5, k+1, n-k-1)$.

Mahalanobis distance - is dedicated to detecting outliers - high values indicate that a case is significantly distant from the center of the independent variables. If a case with the highest Mahalanobis value is found among the cases more than 3 deviations away, it will be marked in bold as the outlier.

We check this assumption visually using a Q-Q plot of the nromal distribution. The large difference between the distribution of the residuals and the normal distribution may disturb the assessment of the significance of the coefficients of the individual variables in the model.

To check if there are areas in which the variance of model residuals is increased or decreased we use the charts of:

  • the residual with respect to predicted values
  • the square of the residual with respect to predicted values
  • the residual with respect to observed values
  • the square of the residual with respect to observed values

For the constructed model to be deemed correct the values of residuals should not be correlated with one another (for all pairs 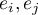$e_i, e_j$). The assumption can be checked by by computing the Durbin-Watson statistic.

\begin{displaymath} d=\frac{\sum_{t=2}^n\left(e_t-e_{t-1}\right)^2}{\sum_{t=1}^ne_t^2}, \end{displaymath}

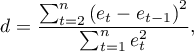
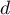To test for positive autocorrelation on the significance level $\alpha$ we check the position of the statistics $d$ with respect to the upper (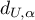$d_{U,\alpha}$) and lower (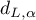$d_{L,\alpha}$) critical value:

  • If 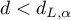$d <d_{L,\alpha}$ – the errors are positively correlated;
  • If 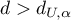$d> d_{U,\alpha}$ – the errors are not positively correlated;
  • If 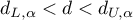$d_{L,\alpha}<d <d_{U,\alpha}$ – the test result is ambiguous.

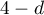To test for negative autocorrelation on the significance level $\alpha$ we check the position of the value $4-d$ with respect to the upper (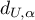$d_{U,\alpha}$) and lower (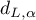$d_{L,\alpha}$) critical value:

  • If 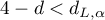$4-d <d_{L,\alpha}$ – the errors are negatively correlated;
  • If 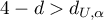$4-d> d_{U,\alpha}$ – the errors are not negatively correlated;
  • If $d_{L,\alpha}<4-d <d_{U,\alpha}$ – the test result is ambiguous.

The critical values of the Durbin-Watson test for the significance level $\alpha=0.05$ are on the website (pqstat) – the source of the: Savin and White tables (1977)1)

EXAMPLE cont. (publisher.pqs file)

1)
Savin N.E. and White K.J. (1977), The Durbin-Watson Test for Serial Correlation with Extreme Sample Sizes or Many Regressors. Econometrica 45, 1989-1996