Sample size determination
For the margin of error of the proportion and the mean
Since it is usually neither practical nor possible to study the entire population, a subset of it - the sample - is chosen. The sample is of course correspondingly smaller than the population, but it should reflect it well. One of the key aspects in planning a study, besides the randomness of the sample, is the assumption of its size. The size should be chosen so that the inference about the population is true.
If we are interested in ensuring that the proportions of certain characteristics, or their mean values, calculated for a sample reflect the proportions or mean values in the population with as little bias as possible, we can estimate the necessary sample size accordingly.
- Sample size for estimating population proportions
Assuming the possibility of an error in estimating the size of 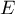 , we can determine the necessary sample size
, we can determine the necessary sample size 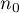 - for an unknown population size or
- for an unknown population size or 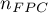 - for a known population size.
- for a known population size.
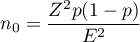
where:
 – the expected proportion in the population specified by the user, whereas - if this quantity is not known, the estimated necessary size will be increased to be sufficient for each possible proportion, so the value
– the expected proportion in the population specified by the user, whereas - if this quantity is not known, the estimated necessary size will be increased to be sufficient for each possible proportion, so the value 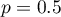 will be used.
will be used.
When we know the population size (and in particular - when the size is relatively small with respect to 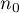 , i.e. when
, i.e. when 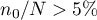 ) we should use the so-called finite population correction (
) we should use the so-called finite population correction (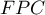 ) (Lenth (2001)1), Armitage and Colton (2009)2)) given by the formula:
) (Lenth (2001)1), Armitage and Colton (2009)2)) given by the formula:
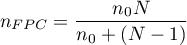
- Sample size for estimating the population mean
Assuming the possibility of an error in estimating the size of 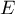 , we can determine the necessary sample size
, we can determine the necessary sample size 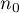 - for an unknown population size or
- for an unknown population size or 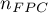 - for a known population size.
- for a known population size.
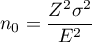
where:
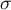 – population standard deviation - known from previous studies.
– population standard deviation - known from previous studies.
When we know the population size (and in particular - when the size is relatively small with respect to 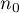 , i.e. when
, i.e. when 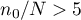 ) we should use the so-called finite population correction (
) we should use the so-called finite population correction (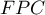 ) given by the formula:
) given by the formula:
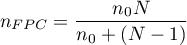
The window with the Sample size determination settings is opened via menu Advanced statistics→test power and sample size→Sample size determination
EXAMPLE Estimation of proportions
Population: Eligible to vote for President of Poland.
We are interested in endorsements of individual candidates.
How many people should be selected so that the resulting percentage has bias of at most 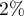 ?
?
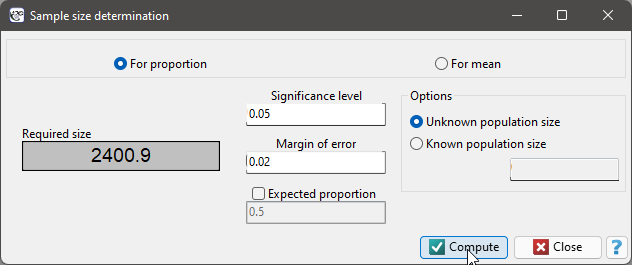
With a sample size of at least 2401 elements, we will have 95% confidence that the bias in support for the selected presidential candidate does not exceed 2%. This means that in 95% of experiments involving drawing a random 2401 element sample from the population, the bias of the support estimate for a given candidate will not exceed 2%, but in 5% of such experiments it may be greater than 2%.
When choosing the size of the acceptable bias, one should pay attention to the fact whether there is not a situation in which candidates with small support (on the limit of the assumed estimation bias) take part in the election. If this is the case, it is worth reducing the value of the estimated bias - the consequence of reducing the bias will then be an increase in the necessary sample size.
EXAMPLE Estimating the mean value
Population: Individuals with hypertension in Poland in 2005-2010, aged 20-40 years.
We are interested in the mean body weight of these individuals.
How many individuals should be selected so that the mean body weight has bias of at most 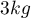 ? We know that the population standard deviation of the body weight of these individuals is
? We know that the population standard deviation of the body weight of these individuals is 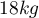 .
.
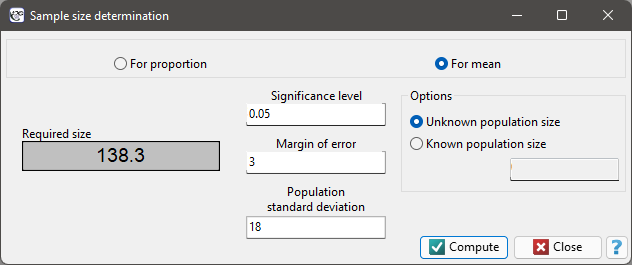
To be 95% sure that there is a population mean within the bias 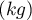 built around the mean of our sample we need to select at least 139 individuals.
built around the mean of our sample we need to select at least 139 individuals.