Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
Action disabled: source
statpqpl:survpl:phcoxpl
Spis treści
Regresja proporcjonalnego hazardu Cox'a
Okno z ustawieniami opcji Regresji Cox'a wywołujemy poprzez menu Statystyka→Analiza przeżycia→Regresja PH Cox'a
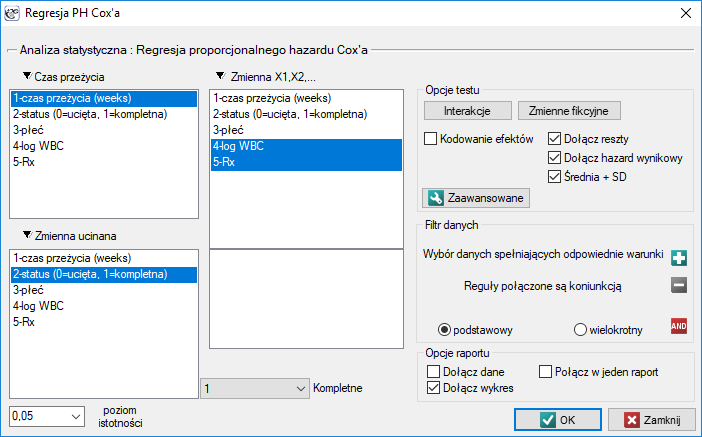
Regresja Cox'a, znana również jako model proporcjonalnego hazardu Cox'a (Cox PH model) - Cox D.R. (1972)1), jest najszerzej stosowanym podejściem regresyjnym w analizie przeżycia. Pozwala na zbadanie wpływu wielu zmiennych niezależnych ( ,
,  ,
,  ,
, 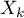 ) na czas przeżycia. Jest to podejście w pewnym sensie nieparametryczne, a więc obarczone niewieloma założeniami - stąd też wynika jego popularność. Nie musi być znana natura ani kształt funkcji hazardu czy przeżycia, a najważniejszy warunek to założenie, które dotyczy również większości parametrycznych modeli przeżycia czyli proporcjonalność hazardu.
) na czas przeżycia. Jest to podejście w pewnym sensie nieparametryczne, a więc obarczone niewieloma założeniami - stąd też wynika jego popularność. Nie musi być znana natura ani kształt funkcji hazardu czy przeżycia, a najważniejszy warunek to założenie, które dotyczy również większości parametrycznych modeli przeżycia czyli proporcjonalność hazardu.
Funkcja, na której oparty jest model proporcjonalnego hazardu Cox'a opisuje hazard wynikowy i jest produktem dwóch wielkości, z których tylko jedna jest zależna od czasu ( ):
):
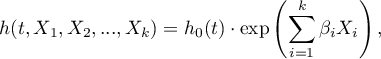 gdzie:
gdzie:
- [
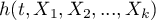 ] - wynikowy hazard opisujący zmieniające się w czasie ryzyko zależne od innych czynników np. sposobu leczenia,
] - wynikowy hazard opisujący zmieniające się w czasie ryzyko zależne od innych czynników np. sposobu leczenia, - [
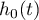 ] - hazard bazowy, czyli hazard przy założeniu, że wszystkie zmienne objaśniające są równe zero,
] - hazard bazowy, czyli hazard przy założeniu, że wszystkie zmienne objaśniające są równe zero,
- [
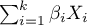 ] - kombinacja (najczęściej liniowa) zmiennych niezależnych i parametrów modelu,
] - kombinacja (najczęściej liniowa) zmiennych niezależnych i parametrów modelu,
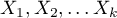 - zmienne objaśniające, niezależne od czasu,
- zmienne objaśniające, niezależne od czasu,
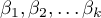 - parametry.
- parametry.
Zmienne fikcyjne i interakcje w modelu
Omówienie przygotowania zmiennych fikcyjnych i interakcji przedstawiono w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Korekcja rang wiązanych w regresji Cox'a oparta jest na metodzie Breslow'a2)
Model można sprowadzić do postaci liniowej:
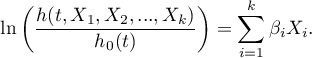
Rozwiązaniem równania jest wówczas wektor ocen parametrów  nazywanych współczynnikami regresji:
nazywanych współczynnikami regresji:
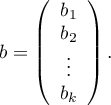
Współczynniki te szacowane są poprzez tzw. „częściową” metodę największej wiarygodności. Jest to metoda „częściowa” ponieważ poszukiwanie maksimum funkcji wiarygodności 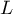 (w programie użyto algorytm iteracyjny Newton-Raphson) odbywa się tylko dla danych kompletnych, dane ucięte są w tym algorytmie uwzględniane, ale nie bezpośrednio.
(w programie użyto algorytm iteracyjny Newton-Raphson) odbywa się tylko dla danych kompletnych, dane ucięte są w tym algorytmie uwzględniane, ale nie bezpośrednio.
Każdy współczynnik obarczony jest pewnym błędem szacunku. Wielkość tego błędu wyliczana jest ze wzoru:
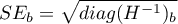
gdzie:
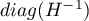 to główna przekątna macierzy kowariancji.
to główna przekątna macierzy kowariancji.
Uwaga!
Budując model należy pamiętać, że liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby szacowanych parametrów modelu ( ) i mniejszej z proporcji liczności uciętych lub kompletnych (
) i mniejszej z proporcji liczności uciętych lub kompletnych ( ), czyli (
), czyli (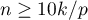 ), Peduzzi P. i inni (1995)3).
), Peduzzi P. i inni (1995)3).
Uwaga! Budując model należy pamiętać, że zmienne niezależne nie powinny być współliniowe. W przypadku gdy występuje współliniowość, estymacja może być niepewna a uzyskane wartości błędów bardzo wysokie.
Uwaga! Kryterium zbieżności funkcji algorytmu iteracyjnego Newtona-Raphsona można kontrolować przy pomocy dwóch parametrów: limitu iteracji zbieżności (podaje maksymalną ilość iteracji w jakiej algorytm powinien osiągnąć zbieżność) i kryterium zbieżności (podaje wartość poniżej której uzyskana poprawa estymacji uznana będzie za nieznaczną i algorytm zakończy działanie).
Przykład c.d. (plik: remisjaBiałaczka.pqs)
Iloraz Hazardu (HR)
Dla każdej zmiennej niezależnej wyliczany jest jednostkowy Iloraz Hazardu (ang. Hazard Ratio - 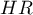 ):
):
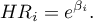 Wyraża on zmianę ryzyka niepożądanego zdarzenia, gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wyraża on zmianę ryzyka niepożądanego zdarzenia, gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wartość 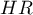 interpretujemy następująco:
interpretujemy następująco:
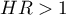 oznacza stymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile wzrasta ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.
oznacza stymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile wzrasta ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.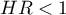 oznacza destymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile spada ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.
oznacza destymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile spada ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.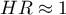 oznacza, że badana zmienna niezależna nie ma wpływu na wystąpienie niepożądanego zdarzenia.
oznacza, że badana zmienna niezależna nie ma wpływu na wystąpienie niepożądanego zdarzenia.
Uwaga!
Jeśli analizę przeprowadzamy dla modelu innego niż liniowy, lub uwzględniamy interakcję, wówczas analogicznie jak w modelu regresji logistycznej na podstawie ogólnego wzoru możemy wyliczyć odpowiedni 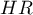 zmieniając formułę będącą kombinacją zmiennych niezależnych.
zmieniając formułę będącą kombinacją zmiennych niezależnych.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu (istotność ilorazu hazardów)
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem Walda.
Hipotezy:
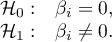
lub równoważnie:
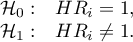
Statystykę testową testu Walda wyliczamy według wzoru:
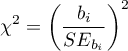
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniem swobody .
stopniem swobody .
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jakość zbudowanego modelu
Dobry model powinien spełniać dwa podstawowe warunki: powinien być dobrze dopasowany i możliwie jak najprostszy. Jakość modelu proporcjonalnego hazardu Cox'a możemy ocenić kilkoma ogólnymi miarami, które opierają się na:
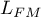 - maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
- maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
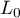 - maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
- maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
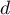 - obserwowanej liczbie niepożądanych zdarzeń.
- obserwowanej liczbie niepożądanych zdarzeń.
Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
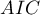 ,
, 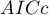 i
i 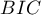 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby parametrów w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby parametrów w modelu ( ) i liczby obserwacji kompletnych (
) i liczby obserwacji kompletnych (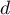 ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby parametrów i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby parametrów i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
- Kryterium informacyjne Akaikego (ang. Akaike information criterion)
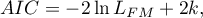
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób.
- Poprawione kryterium informacyjne Akaikego
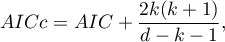
Poprawka kryterium Akaikego dotyczy wielkości próby (liczby zdarzeń niepożądanych), przez co jest to miara rekomendowana również dla prób o małych licznościach.
- Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
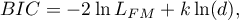
Podobnie jak poprawione kryterium Akaikego uwzględnia wielkość próby (liczbę zdarzeń niepożądanych) - Volinsky i Raftery 2000r4)
Pseudo R - tzw. McFadden
- tzw. McFadden  jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej
jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej  wyznaczanego dla liniowej regresji wielorakiej).
wyznaczanego dla liniowej regresji wielorakiej).
Wartość tego współczynnika mieści się w przedziale 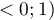 , gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,
, gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu, 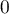 - zupełny bark dopasowania. Współczynnik
- zupełny bark dopasowania. Współczynnik 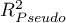 wyliczamy z wzoru:
wyliczamy z wzoru:
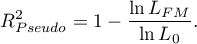
Ponieważ współczynnik 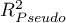 nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
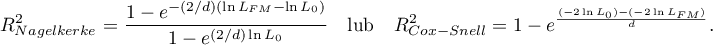
Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test ilorazu wiarygodności. Test ten weryfikuje hipotezę:
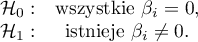
Statystyka testowa ma postać:
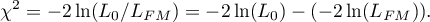
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

AUC – pole pod krzywą ROC – Krzywa ROC – zbudowana na podstawie informacji o wystąpieniu zdarzenia lub jego braku oraz kombinacji zmiennych niezależnych i parametrów modelu – pozwala na ocenę zdolności zbudowanego modelu regresji Cox'a do klasyfikacji przypadków do dwóch grup: (1 – zdarzenie) i (0 – brak zdarzenia). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej
, to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej  , czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą
, czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą  , zatem większe niż
, zatem większe niż 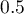
Hipotezy:
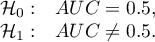
Statystyka testowa ma postać:
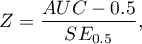 gdzie:
gdzie:
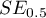 - błąd pola.
- błąd pola.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, dla krzywej ROC podawana jest proponowana wartość punktu odcięcia kombinacji zmiennych niezależnych i parametrów modelu.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
Analiza reszt modelu
Analiza reszt modelu pozwala na weryfikację jego założeń. Głównym jej celem w regresji Cox'a jest lokalizacja wartości odstających i badanie proporcjonalności hazardu. Standardowo w modelach regresji reszty oblicza się jako różnice obserwowanych i przewidywanych przez model wartości zmiennej zależnej. Jednakże w przypadku występowania zmiennych uciętych taka koncepcja wyznaczania reszt nie jest odpowiednia. W programie można analizować reszty opisywane jako: Martingale, Deviance, Schoenfeld. Reszty te można wyrysowywać względem czasu lub zmiennych niezależnych.
Założenie proporcjonalności hazardu
Opracowano szereg graficznych metod pozwalających na ocenę adekwatności modelu proporcjonalnego hazardu (Lee i Wang 20035)). Najszerzej stosowane są metody bazujące na resztach modelu. Podobnie jak inne graficzne metody oceny proporcjonalności hazardu jest to metoda subiektywna. Aby założenie proporcjonalnego hazardu było spełnione reszty względem czasu nie powinny układać się w żaden wzór ale powinny być losowo rozłożone w okolicach wartości 0.
Martingale - reszty te mogą być interpretowane jako różnica w czasie ![LaTeX $[0,t]$](/lib/exe/fetch.php?media=wiki:latex:/img990afe3dc2a01ee124e9c8ef79e63b21.png) pomiędzy obserwowaną licznością zdarzeń niepożądanych i przewidywaną przez model licznością tych zdarzeń. Wartość oczekiwana dla tych reszt to 0, ale ich wadą jest skośny rozkład utrudniający interpretację ich wykresu (zawierają się w przedziale od
pomiędzy obserwowaną licznością zdarzeń niepożądanych i przewidywaną przez model licznością tych zdarzeń. Wartość oczekiwana dla tych reszt to 0, ale ich wadą jest skośny rozkład utrudniający interpretację ich wykresu (zawierają się w przedziale od 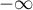 do 1).
do 1).
Deviance - podobnie jak Martingale asymptotycznie uzyskują wartość oczekiwaną równą 0, ale rozkładają się symetrycznie wokół zera z odchyleniem standardowym równym 1, gdy dopasowywany model jest odpowiedni. Wartość Deviance jest dodatnia, gdy obiekt badany przeżywa krócej niż oczekiwany na podstawie modelu czas, a ujemna gdy ten czas jest dłuższy. Analiza tych reszt jest wykorzystywana w badaniu proporcjonalności hazardu - ale jest to przede wszystkim narzędzie identyfikujące wartości odstające. W raporcie reszt, te z nich, które są oddalone o więcej niż 3 odchylenia standardowe od 0 oznaczone są kolorem czerwonym.
Schoenfeld - reszty te wyliczane są oddzielnie dla każdej zmiennej niezależnej i definiowane tylko dla obserwacji kompletnych. Dla każdej zmiennej niezależnej suma reszt Schoenfeld'a i ich wartość oczekiwana to 0. Zaletą przedstawiania reszt względem czasu dla każdej zmiennej jest możliwość zidentyfikowania zmiennej nie spełniającej w modelu założenia proporcjonalności hazardu. Jest to ta zmienna, której wykres reszt układa się w systematyczny wzór (najczęściej bada się tu liniową zależność reszt od czasu). Równomierne rozłożenie punktów względem wartości 0 świadczy o braku zależności reszt od czasu - czyli spełnieniu założenia proporcjonalności hazardu przez daną zmienną w modelu.
Gdy dla którejkolwiek zmiennej w modelu Cox'a nie jest spełnione założenie proporcjonalności hazardu, jednym z możliwych rozwiązań jest wykonanie analizy Cox'a oddzielnie dla każdego poziomu tej zmiennej.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
1)
Cox D.R. (1972), Regression models and life tables. Journal of the Royal Statistical Society, B34:187-220
2)
Breslow N.E. (1974), Covariance analysis of censored survival data. Biometrics, 30(1):89–99
3)
Peduzzi P., Concato J., Feinstein A.R., Holford T.R. (1995), Importance of events per independent variable in proportional hazards regression analysis. II. Accuracy and precision of regression estimates. Journal of Clinical Epidemiology, 48:1503-1510
4)
Volinsky C.T., Raftery A.E. (2000) , Bayesian information criterion for censored survival models. Biometrics, 56(1):256–262
5)
Lee E. T., Wang J. W. (2003), Statistical Methods for Survival Data Analysis, ed. third, Wiley
statpqpl/survpl/phcoxpl.txt · ostatnio zmienione: 2023/10/27 21:54 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


