PQStat - Baza Wiedzy

Trend w krzywych przeżycia

Hipotezy:

$\begin{array}{ll} \mathcal{H}_0: & $W badanej populacji nie istnieje trend w położeniu krzywych $S_1,S_2,...,S_k,\\ \mathcal{H}_1: & $W badanej populacji istnieje trend w położeniu krzywych $S_1,S_2,...,S_k. \end{array}$

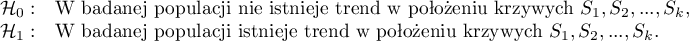
W obliczeniach wykorzystano statystykę chi-kwadrat postaci:

$\begin{displaymath} \chi^2=\frac{(c'U)^2}{c'Vc} \end{displaymath}$

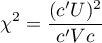
gdzie:

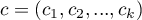
$c=(c_1,c_2,...,c_k)$ $-$ wektor wag dla porównywanych grup informujący o ich naturalnym porządku (najczęściej kolejne liczby naturalne).

Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z jednym stopniem swobody. Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Uwaga!

By można było przeprowadzić analizę trendu w krzywych przeżycia, zmienna grupująca musi być zmienną liczbową, w której wartości liczb informują o naturalnym porządku grup. Liczby te w analizie traktowane są jako wagi 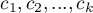$c_1,c_2,...,c_k$ .

Przykład c.d. (plik przeszczep.pqs)

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Trend w krzywych przeżycia

Narzędzia strony