statpqpl:wielowympl:mediacja

Efekt mediacji

Baron i Kenny (1986)¹⁾ zdefiniowali mediatora (M) jako zmienną wyjaśniającą w istotny sposób relację między zmienną niezależną (X) a zmienną wynikową (Y). W mediacji zakłada się, że związek między zmienną niezależną a zmienną zależną jest efektem pośrednim, który istnieje dzięki wpływowi trzeciej zmiennej (mediatora).

$\begin{pspicture}(-0.5,-0.5)(4,3.5) \psline{->}(0.2,3)(2.8,3) \rput(-2,3){\scriptsize model jednowymiarowy} \rput(0,2.8){\scriptsize \textbf{X}} \rput(3,2.8){\scriptsize \textbf{Y}} \rput(1.5,2.7){\scriptsize $\tau$} \rput(-2,0){\scriptsize model wielowymiarowy} \rput(0,0){\scriptsize \textbf{X}} \rput(3,0){\scriptsize \textbf{Y}} \rput(1.5,2){\scriptsize \textbf{M}} \psline[linewidth=0.7pt, linestyle=dotted]{->}(0.2,0.2)(1.2,1.8) \psline[linewidth=0.7pt, linestyle=dotted]{->}(1.8,1.8)(2.8,0.2) \psline{->}(0.2,0)(2.8,0) \rput(0.4,1){\scriptsize \textit{a}} \rput(2.6,1){\scriptsize \textit{b}} \rput(1.5,-0.2){\scriptsize $\tau'$} \end{pspicture}$

Wielkość zmian określamy poprzez różnicę współczynników opisujących związek zmiennej X ze zmienną Y w modelu jednowymiarowym:

$Y=\tau\cdot X+c$

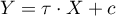
i w modelu wielowymiarowym, czyli uwzględniającym zmienną M:

$Y=\tau'\cdot X+b\cdot M+c$ .

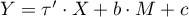Różnica:

$\begin{displaymath} \tau-\tau'=a\cdot b \end{displaymath}$

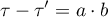
Efekt mediacji:

$\begin{displaymath} \frac{\tau-\tau'}{\tau}\cdot 100\% \end{displaymath}$

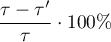
W rezultacie, gdy mediator (M) jest włączony do modelu regresji określającego związek zmiennej X i Y, wpływ zmiennej niezależnej 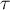$\tau$ jest zmniejszony do $\tau'$ .

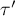Testy oceniające efekt mediacji

Test Sobela (1982)²⁾, test Aroiana (1947)³⁾ spopularyzowany przez Barona i Kennyiego ⁴⁾ oraz test Goodmana (1960)⁵⁾ są testami, które określają, czy zmniejszenie wpływu zmiennej niezależnej na zmienną wynikową, po uwzględnieniu mediatora w modelu, jest znaczną redukcją, a zatem czy efekt mediacji jest istotny statystycznie.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & \tau = \tau'\\ \mathcal{H}_1: & \tau \ne \tau', \end{array}$

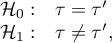
Statystyka testowa dla testu Sobela ma postać:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b}} \end{displaymath}$

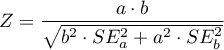
Statystyka testowa dla testu Aroiana ma postać:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b + SE^2_a\cdot SE^2_b}} \end{displaymath}$

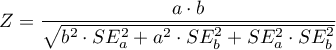
Statystyka testowa dla testu Goodmana ma postać:

$\begin{displaymath} Z=\frac{a\cdot b}{\sqrt{b^2\cdot SE^2_a+ a^2 \cdot SE^2_b - SE^2_a\cdot SE^2_b}} \end{displaymath}$

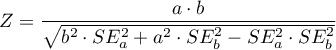
Statystyki te mają asymptotycznie (dla dużych liczności) rozkład normalny.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Uwaga!

Test Sobela, jak też test Aroiana i Goodmana, są to testy bardzo konserwatywne i przeznaczone jedynie dla dużych prób (przekraczających 100 elementów).

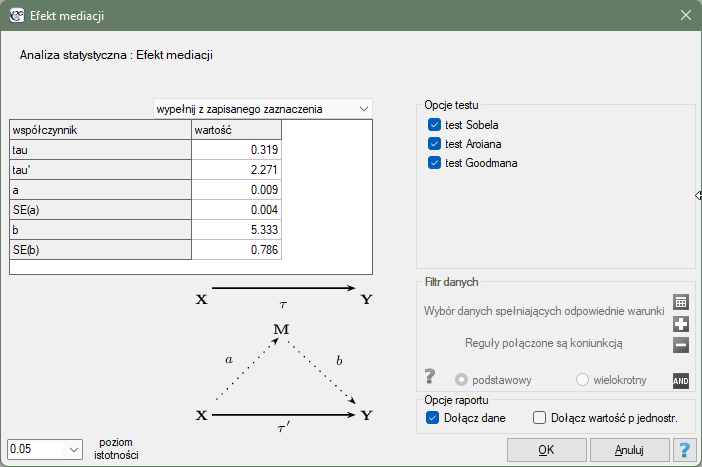
Okno Analizy efektu mediacji wywołujemy poprzez:

Statystyki zaawansowane→Modele wielowymiarowe→Efekt mediacji.

Przykład

Na podstawie pracy Mimar Sinan Fine (2017) ⁶⁾.

Badanie obejmuje 300 osób dorosłych mieszkających w Stambule. Zmienna zależna Y to ciśnienie skurczowe, a zmienna niezależna X to wiek. Zmienna pośrednicząca M to częstotliwość spożywania alkoholu. Celem pracy jest zbadanie zależności między wiekiem a skurczowym ciśnieniem krwi oraz przedstawienie wpływu częstości spożywania alkoholu na tę zależność.

Zbudowano model jednowymiarowy, w którym nie uwzględniono potencjalnego mediatora:

$Y=0.319 \cdot X+c$ .

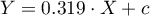Wielkość wpływu zmiennej X (wiek) na zmienną Y (ciśnienie skurczowe) wyniosła tau=0.319.

Zbudowano model wielowymiarowy, w którym uwzględniono potencjalny mediator:

$Y=2.271 \cdot X + 5.333\cdot M+c$ .

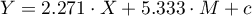Wielkość wpływu zmiennej X (wiek) na zmienną Y (ciśnienie skurczowe) wyniosła tau'=2.271. Wiemy również z tego modelu iż b=5.333, a błąd 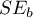$SE_b$ =0.786

Różnica między współczynnikami to tau-tau'= a*b=0.048. Efekt mediacji wynosi (tau-tau')/tau=(0.319-0.271)/0.371=0.15047, co oznacza, że M (częstość spożycia alkoholu) modyfikuje badany związek zmniejszając współczynnik o około 15%.

Zbudowano model jednowymiarowy badający wpływ zmiennej X na mediator:

$M=0.009\cdot X+c$ .

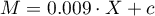Wiemy z tego modelu, że współczynnik a=0.009, a błąd 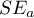$SE_a$ =0.004. Wszystkie te informacje wprowadzamy w oknie analizy uzyskując następujący raport:

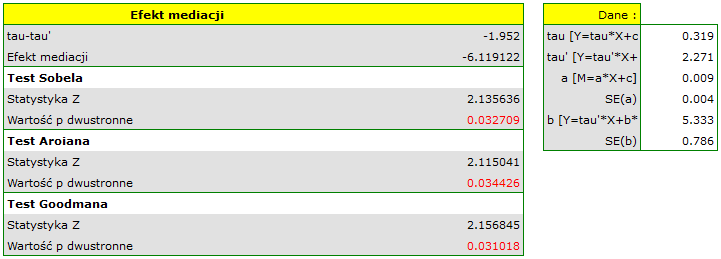
Na podstawie współczynników a i b oraz ich błędów standardowych wyznaczony zostaje wynik testów Sobela (p=0.0327), Aroiana (p=0.0344) i Goodmana (p=0.0310). Uzyskane wartości p wskazują na istotne statystycznie znaczenie mediatora. Potwierdziliśmy więc, że częstość spożywania alkoholu wpływa na związek wieku z ciśnieniem rozkurczowym na tyle zauważalnie, że warto wyjaśniać dlaczego ten efekt występuje.

¹⁾ , ⁴⁾

Baron R. M., Kenny D. A. (1986), The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology, 51, 1173-1182.

²⁾

Sobel M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology 13: 290–312

³⁾

Aroian, L. A. (1947), The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics, 18, 265-271.

⁵⁾

Goodman L. A. (1960), On the exact variance of products. Journal of the American Statistical Association, 55, 708-713

⁶⁾

Mimar S.F. (2017), The Mediation Analysis With the Sobel Test and the Percentile Bootstrap, International Journal of Management and Applied Science, Volume-3, Issue-2