Inne atrybuty rozkładu

Skośność inaczej współczynnik asymetrii (ang. skewness)

Jest to miara, która mówi o tym jak bardzo rozkład danych różni się od rozkładu symetrycznego. Im wartość współczynnika asymetrii jest bliższa zeru, tym bardziej symetrycznie wokół średniej rozkładają się dane. Zwykle wartość tego współczynnika zawiera się w przedziale [-1, 1], chociaż może w przypadku szczególnie dużej asymetrii znaleźć się poza tym przedziałem. Wartości dodatnie świadczą o występowaniu skośności prawostronnej (o dłuższym prawym „ogonie”) wartości ujemne zaś o skośności lewostronnej (o dłuższym lewym „ogonie”). Skośność wyraża się wzorem: \begin{displaymath} A=\frac{n}{(n-1)(n-2)}\sum_{i=1}^n\left(\frac{x_i-\overline{x}}{sd}\right)^3, \end{displaymath}

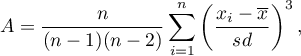
gdzie:

$x_i$ – kolejne wartości zmiennej,

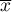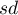$\overline{x}$, $sd$ – odpowiednio średnia arytmetyczna i odchylenie standardowe $x_i$,

$n$ – liczność próby.

\begin{tabular}{cc} \begin{pspicture}(0,-.7)(7,3.6) \rput(2.5,3.3){skośność prawostronna} \rput(2.8,2.8){$A>0$} \psline{->}(0,0)(0,3) \psline{->}(0,0)(6.3,0) \psbezier{-}(.2,.2)(.5,.2)(.7,2.3)(1.3,2.5) \psbezier{-}(1.3,2.5)(2,2.5)(3,.2)(5.3,.2) \psline[linestyle=dotted]{-}(2.2,0)(2.2,1.7) \rput(2.55,-.3){Med.} \psline[linestyle=dotted]{-}(1.3,0)(1.3,2.5) \rput(1.3,-.3){Moda} \psline[linestyle=dotted]{-}(3.4,0)(3.4,.7) \rput(3.5,-.3){$\overline{X}$} \rput{90}(-.4,2.7){częstość} \rput(6.1,-.3){x} \end{pspicture} & \begin{pspicture}(0,-.7)(7,3.6) \rput(2.5,3.3){skośność lewostronna} \rput(2.2,2.8){$A<0$} \psline{->}(0,0)(0,3) \psline{->}(0,0)(6.3,0) \psbezier{-}(.2,.2)(2.1,.2)(2.8,2.5)(3.7,2.5) \psbezier{-}(3.7,2.5)(4.2,2.5)(4.8,.2)(5.5,.2) \psline[linestyle=dotted]{-}(2.85,0)(2.85,1.75) \rput(2.7,-.3){Med.} \psline[linestyle=dotted]{-}(3.7,0)(3.7,2.5) \rput(3.9,-.3){Moda} \psline[linestyle=dotted]{-}(1.7,0)(1.7,.7) \rput(1.7,-.3){$\overline{X}$} \rput{90}(-.4,2.7){częstość} \rput(6.1,-.3){x} \end{pspicture} \end{tabular}

Kurtoza inaczej współczynnik koncentracji (ang. kurtosis)

Jest to miara, która mówi o tym jak bardzo rozrzut danych wokół średniej jest zbliżony do rozrzutu tych danych w rozkładzie normalnym. Im wartość kurtozy jest większa od zera, tym badany rozkład jest bardziej smukły niż rozkład normalny a im wartość kurtozy jest mniejsza od zera, tym badany rozkład jest bardziej spłaszczony niż rozkład normalny. Kurtoza wyraża się wzorem: \begin{displaymath} K=\frac{n(n+1)}{(n-1)(n-2)(n-3)}\sum_{i=1}^n\left(\frac{x_i-\overline{x}}{sd}\right)^4-\frac{3(n-1)^2}{(n-2)(n-3)}, \end{displaymath}

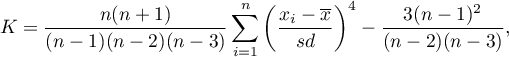
gdzie:

$x_i$ – kolejne wartości zmiennej,

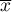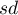$\overline{x}$, $sd$ – odpowiednio średnia arytmetyczna i odchylenie standardowe $x_i$,

$n$ – liczność próby.

\begin{pspicture}(0,-.8)(6.5,3.4) \rput(4.0,.7){$K_1<0$} \rput(4.5,2.5){$K_2>0$} \psline{->}(0,0)(0,3) \psline{->}(0,0)(7,0) \psbezier[linestyle=dashed]{-}(.2,.2)(2.2,.8)(2.3,1.4)(3.2,1.5) \psbezier[linestyle=dashed]{-}(3.2,1.5)(4.1,1.4)(4.2,.8)(6.2,.2) \psbezier{-}(.4,.2)(2.4,.6)(2.5,3.0)(3.2,3.1) \psbezier{-}(3.2,3.1)(3.9,3.0)(4.0,.6)(6.0,.2) \psline[linestyle=dotted]{-}(3.2,0)(3.2,3.1) \rput(3.2,-.3){$\overline{X}$} \rput{90}(-.4,2.7){częstość} \rput(6.8,-.3){x} \end{pspicture}

Przykład (plik nawozy.pqs)

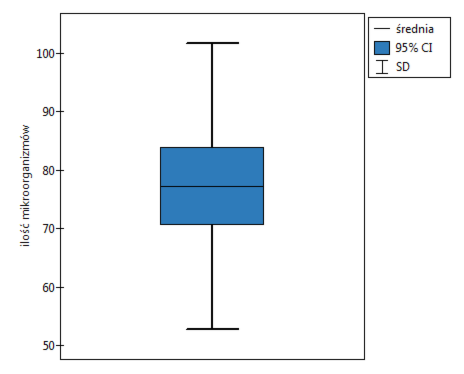
W doświadczeniu dotyczącym nawożenia gleby różnymi rodzajami preparatów mikrobiologicznych i nawozów wyliczono ilość mikroorganizmów występujących w 1 gramie suchej masy gleby. Chcemy wyznaczyć statystyki opisowe ilości promieniowców dla próbki nawożonej azotem i zobrazować uzyskane wyniki za pomocą wykresu ramka-wąsy. Zaznaczamy w arkuszu danych tylko 54 pierwsze wiersze, które odpowiadają założeniom analizy (są to promieniowce nawożone azotem) i uruchamiamy okno Statystyki opisowe poprzez menu Statystyka→Statystyki opisowe.

W oknie opcji testu statystyk opisowych wybieramy zmienną do analizy: Ilość mikroorganizmów, a następnie procedury jakie chcemy wykonać (np. średnią arytmetyczną wraz z przedziałem ufności, medianę, odchylenie standardowe wraz z przedziałem ufności oraz informacje o skośności i kurtozie rozkładu wraz z błędami). Na górze okna powinien być widoczny komunikat:

Dane ograniczone przez zaznaczenie

By w raporcie znalazł się również wykres, zaznaczamy opcję Dołącz wykres i wybieramy interesujący nas rodzaj wykresu ramka-wąsy. Potwierdzamy wybór przyciskiem OK i uzyskujemy wynik w postaci raportu: