Porównywanie modeli regresji PH Cox'a

Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka→Analiza przeżycia→Regresja PH Cox'a - porównywanie modeli

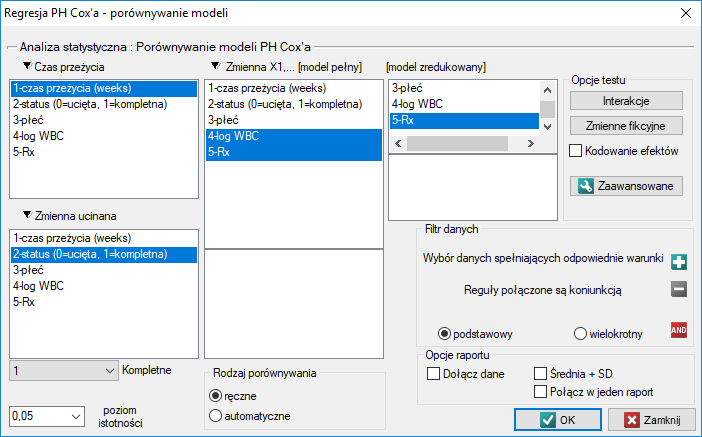
Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji Cox'a, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie związane z czasem przeżycia i słabo skorelowane między sobą.

Porównując modele z różną liczbą zmiennych niezależnych zwracamy uwagę na kryteria informacyjne (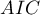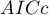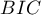$AIC$, $AICc$, $BIC$) oraz współczynniki dopasowania modelu (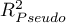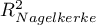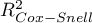$R_{Pseudo}^2$, $R^2_{Nagelkerke}$, $R^2_{Cox-Snell}$). Modele porównywane są również przy użyciu testu ilorazu wiarygodności.

Hipotezy:

\begin{array}{cc} \mathcal{H}_0: & L_{FM}=L_{RM},\\ \mathcal{H}_1: & L_{FM}\ne L_{RM}, \end{array}

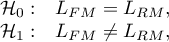
gdzie:

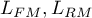$L_{FM}, L_{RM}$ - maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).

Statystyka testowa ma postać:

\begin{displaymath} \chi^2=-2\ln(L_{RM}/L_{FM})=-2\ln(L_{RM})-(-2\ln(L_{FM})) \end{displaymath}

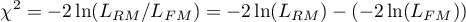
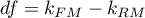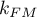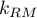Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z $df=k_{FM}-k_{RM}$ stopniami swobody, gdzie $k_{FM}$ i $k_{RM}$ to ilość szacowanych parametrów w porównywanych modelach.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$:

\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}

Decyzję o tym, który model wybrać podejmujemy na podstawie wielkości: 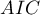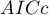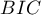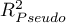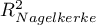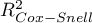$AIC$, $AICc$, $BIC$, $R_{Pseudo}^2$, $R^2_{Nagelkerke}$, $R^2_{Cox-Snell}$ oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym $R^2$) jest istotnie lepszy niż drugi.

W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.

Ręczne porównywanie modeli - polega na zbudowaniu 2 modeli:

pełnego - modelu z większą liczbą zmiennych,

zredukowanego - modelu z mniejszą liczbą zmiennych $-$ model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.

Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.

Automatyczne porównywanie modeli jest wykonywane w kilku krokach:

[krok 1] Zbudowanie modelu z wszystkich zmiennych.

[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.

[krok 3] Porównanie modelu pełnego i zredukowanego.

[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.

[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.

[…]

W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.

Przykład (plik: remisjaBiałaczka.pqs)

Analiza opiera się na danych dotyczących białaczki opisanych w pracy Freireich i innych 19631) i analizowanych dalej przez wielu autorów min. Kleinbaum i Klein 20052)). Dane zawierają informację o czasie (w tygodniach) pozostawania w remisji aż do momentu wycofania pacjenta z badania z powodu wyjścia z remisji (nawrotu objawów) lub ucięcia informacji o pacjencie. Wyjście z remisji jest nastąpieniem zdarzenia niekorzystnego - traktowane jest jako obserwacja kompletna. Obserwacja jest ucięta jeśli pacjent pozostaje w badaniu do końca i remisja nie nastąpi lub jeśli opuści badanie.

Pacjenci przydzieleni zostali do dwóch grup: grupy leczonej tradycyjnie (oznaczonej jako 1 i czasami nazywanej „grupą placebo” ) i grupy leczonej nową metodą (oznaczonej jako 0). Zebrano informację o płci pacjentów (1=mężczyzna, 0=kobieta) oraz o wartościach wskaźnika określającego liczbę białych krwinek oznaczonego jako „log WBC”, który jest znanym czynnikiem prognostycznym.

Celem badania jest określenie wpływu sposobu leczenia na czas pozostawania w remisji przy uwzględnieniu możliwych czynników wikłających (confounder) i interakcji. W analizie uwagę skupimy na zmiennej „Rx (1=placebo, 0=new treatment) ”, zmienną „log WBC” umieścimy w modelu jako możliwy czynnik wikłający (modyfikujący uzyskany efekt). By ocenić ewentualny wpływ interakcji „Rx” i „log WBC” rozważymy także trzecią zmienną będącą iloczynem zmiennych wchodzących w skład interakcji. Zmienną tę dołączymy do modelu wybierając w oknie analizy przycisk Interakcje i dokonując odpowiednich ustawień.

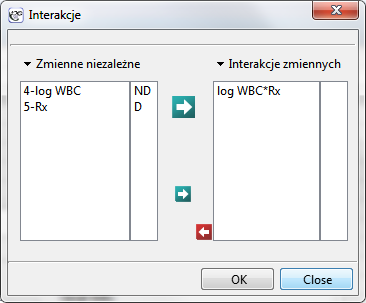
Budujemy trzy modele Coxa:

  • [Model A] zawiera tylko zmienną „Rx”

  • [Model B] zawiera zmienną „Rx” i potencjalną zmienną wikłającą „log WBC”

  • [Model C] zawiera zmienną „Rx” zmienną „log WBC” oraz potencjalny efekt interakcji tych zmiennych: „Rx 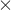$\times$ log WBC”

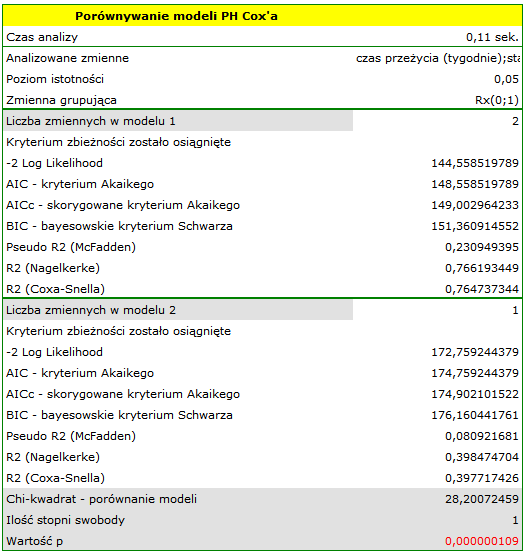
Zmienna mówiąca o interakcji „Rx” i „log WBC”, zawarta w modelu C jest w nim nieistotna (p=0.5103) według testu Walda. Możemy więc uznać za zbyteczne dalsze rozważanie w modelu interakcji tych dwóch zmiennych. Podobne wyniki uzyskamy porównując testem Ilorazu Wiarygodności model C z modelem B. Porównanie to możemy wykonać wybierając menu Regresja Cox'a - porównywanie modeli, uzyskamy wówczas wynik nieistotny (p=0.5134), co oznacza, że model C (model z interakcją) jest NIEistotnie lepszy niż model B (model bez interakcji).

Odrzucamy więc model C przechodząc do rozważania modelu B i modelu A.

HR dla „Rx” w modelu B wynosi 3.65, co oznacza, że hazard dla „grupy placebo” jest około 3.6 większy niż dla grupy pacjentów leczonych nową metodą. Model A zawiera tylko zmienną „Rx”, przez co nazywany jest zwykle modelem „surowym” (ang. crude model) ponieważ ignoruje efekt potencjalnych zmiennych wikłających. W modelu tym HR dla „Rx” wynosi 4.52 i jest sporo większe niż w modelu B. Przyjrzyjmy się jednak nie tylko punktowym wartościom estymatora HR ale również 95\% przedziałowi ufności dla tych estymatorów. Przedział dla „Rx” w modelu A ma szerokość 8.06 (10.09 minus 2.03) a w modelu B jest węższy: 6.74 (8.34 minus 1.60). Dlatego model B daje bardziej precyzyjną estymację HR niż model A. By ostatecznie zdecydować, który model (model A czy model B) będzie lepszy w oszacowaniu efektu leczenia („Rx”) ponownie wykonujemy analizę porównawczą modeli w module Regresja Cox'a - porównywanie modeli. Tym razem test Ilorazu Wiarygodności daje wynik istotny (p<0.0001), co ostatecznie potwierdza wyższość modelu B. Jest to model o najniższej wartości kryteriów informacyjnych (AIC=148.6, AICc=149 BIC=151.4) i wysokich wartościach dopasowania modelu (Pseudo 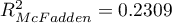$R^2_{McFadden}=0.2309$, $R^2_{Nagelkerke}=0.7662$, $R^2_{Coxa-Snella}=0.7647$).

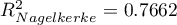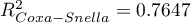Dopełnieniem powyższej analizy jest przedstawienie dla modelu B krzywych przeżycia (pozostawania w remisji) obu grup: leczonej nowym lekiem i tradycyjnie, skorygowanych o wpływ „log WBC”. Na wykresie obserwujemy różnice między grupami, występujące w poszczególnych punktach osi czasu. By wyrysować takie krzywe, po wybraniu opcji Dołącz wykres zaznaczamy opcję Funkcja przeżycia: w podgrupach … a nastęnie, by szybko zbudować wykres dwóch krzywych wybieram Szybkie podgrupy i wskazuję zmienną Rx. Opcja Zaawansowane podgrupy pozwala na zbudowanie dowolnej liczby dowolnie zdefiniowanych krzywych.

Na koniec ocenimy założenia regresjii Cox'a analizując reszty modelu względem czasu.

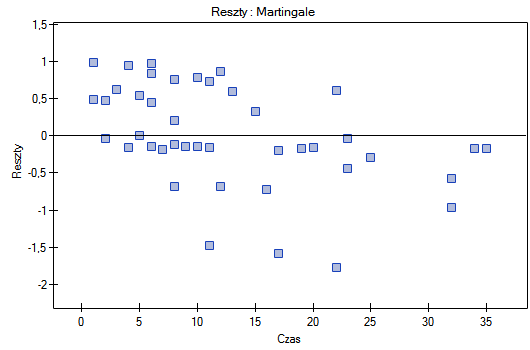
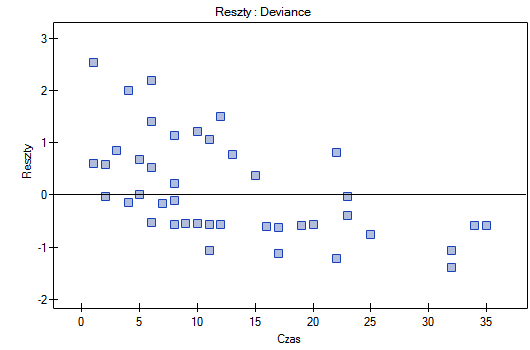
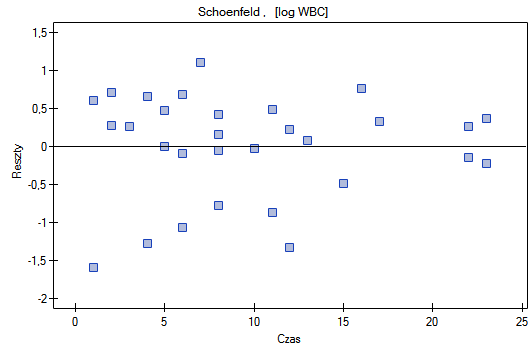
Nie obserwujemy odstających punktów, aczkolwiek reszty Martingale i Deviance są coraz niższe dla coraz dłuższego czasu. Natomiast reszty Schoenfeld'a przedstawiają symetryczny rozkład względem czasu. W przypadku reszt Schoenfeld'a analizę wykresu można wesprzeć różnego rodzaju testami mogącymi ocenić, czy punkty wykresu reszt układają się w pewien wzór np. zależność liniową. By tej analizy dokonać należy przekopiować reszty Schoenfeld'a oraz czas do arkusza danych i przetestować szukany rodzaj zależności. Wynik takiego testu dla każdej zmiennej wskazuje na spełnienie założenia proporcjonalności hazardu przez daną zmienną w modelu - gdy jest nieistotny statystycznie lub złamanie tego założenia - gdy jest istotny statystycznie. W rezultacie zmienną łamiącą założenia regresji proporcjonalnego hazardu Cox'a można wyłączyć z modelu. W przypadku zmiennych „Log WBC” i „Rx” symetryczny rozkład reszt sugeruje spełnienie założenia proporcjonalności hazardu przez te zmienne. Potwierdzeniem tego może być sprawdzenie zależności np. liniowej Pearsona, lub monotonicznej Spearmana dla tych reszt i czasu.

Dalej możemy dodać do modelu zmienną płeć. Musimy jednak postępować ostrożnie, gdyż na podstawie różnych źródeł wiadomo, że płeć może wpływać na funkcję przeżycia (pozostawania w remisji) dotyczącą białaczki w ten sposób, że funkcje przeżycia mogą układać się nieproporcjonalnie względem siebie wzdłuż osi czasu. Wykonujemy więc model Cox'a dla trzech zmiennych: zmiennej „Płeć”, „Rx” i „log WBC”. Zanim dokonamy interpretacji współczynników modelu sprawdzimy reszty Shoenfeld'a. Reszty przedstawiamy na wykresach, a wyniki reszt Shoenfeld'a oraz czasu przekopiujemy z raportu do nowego arkusza, gdzie sprawdzimy występowanie zależności monotonicznej Spearmana. W wyniku uzyskujemy wartość p=0.0259 (dla zależności czasu i reszt Shoenfeld'a dla płci), p=0.6192 (dla zależności czasu i reszt Shoenfeld'a dla log WBC) i p=0,1490 (dla zależności czasu i reszt Shoenfeld'a dla Rx) co potwierdza naruszenie założenia proporcjonalności hazardu przez zmienną płeć. Model Cox'a zbudujemy więc oddzielnie dla kobiet i mężczyzn. W tym celu analizę wykonamy dwukrotnie z włączonym filtrem danych. Za pierwszym razem filtr będzie wskazywał płeć żeńską (0), a za drugim razem płeć męską (1).

Dla kobiet

Dla mężczyzn

1)
Freireich E.O., Gehan E., Frei E., Schroeder L.R., Wolman I.J., et al. (1963), The effect of 6-mercaptopmine on the duration of steroid induced remission in acute leukemia. Blood, 21: 699–716
2)
Kleinbaum D. G., Klein M., (2005) Survival Analysis: A Self-Learning Text, Second Edition (Statistics for Biology and Health