Wiele informacji, które niosą współczynniki zwracane w tabelach można przedstawić na jednym wykresie. Umiejętność czytania wykresów pozwala na szybką interpretację wielu aspektów przeprowadzonej analizy. Wykresy zbierają w jednym miejscu informację dotyczącą wzajemnych relacji pomiędzy składowymi, zmiennymi pierwotnymi i przypadkami. Dają całościowy obraz analizy składowych głównych, przez co są bardzo dobrym jej podsumowaniem.

Wykres ładunków czynnikowych

Wykres przedstawia wektory połączone z początkiem układu współrzędnych, które to reprezentują zmienne pierwotne. Wektory te są umieszczone na płaszczyźnie wyznaczonej przez dwie wybrane składowe główne.

• Współrzędne końca wektora to odpowiadające im ładunki czynnikowe zmiennych.

• Długość wektora reprezentuje zasób informacyjny zmiennej pierwotnej, jaki niosą składowe główne wyznaczające układ współrzędnych. Im dłuższy wektor, tym wkład zmiennej pierwotnej w budowę składowych większy. W przypadku analizy opartej na macierzy korelacji ładunki są korelacjami pomiędzy zmiennymi pierwotnymi a składowymi, wówczas punkty wpadają do koła jednostkowego. Dzieje się tak dlatego, że współczynnik korelacji nie może przekroczyć jedynki. W rezultacie, im dana zmienna pierwotna leży bliżej brzegu tego koła, tym lepsza jest jej reprezentacja przez przedstawione główne składowe.

• Znak współrzędnych końca wektora czyli znak ładunku czynnikowego - wskazuje na dodatnią lub ujemną korelację zmiennej pierwotnej i składowych głównych tworzących układ współrzędnych. Jeżeli rozpatrujemy łącznie obie osie (2 składowe), wówczas zmienne pierwotne mogą być kwalifikowane do jednej z czterech kategorii, zależnie od kombinacji znaków (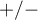) ich ładunków czynnikowych.

• Kąt między wektorami wskazuje na skorelowanie zmiennych pierwotnych:
  
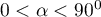  : im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest mniejszy tym silniejsza jest dodatnia korelacja pomiędzy tymi zmiennymi.
  
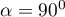  - wektory te są prostopadłe, czyli zmienne pierwotne nie są skorelowane.
  
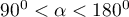  - im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest większy, tym silniejsza jest ujemna korelacja pomiędzy tymi zmiennymi.

Biplot

Wykres przedstawia 2 serie danych umieszczone w układzie współrzędnych wyznaczonych przez 2 składowe główne. Serię pierwszą na wykresie stanowią dane z wykresu pierwszego (czyli wektory zmiennych pierwotnych) a serię drugą punkty przedstawiające poszczególne przypadki.

• Współrzędne punktów powinny być interpretowane jak wartości zestandaryzowane, tzn. współrzędne dodatnie wskazują na wartość wyższą od średniej wartości składowej głównej, ujemne na wartość niższą a im wyższa wartość bezwzględna tym dalej punkty znajdują się od średniej. Przy czym, jeśli na wykresie znajdują się obserwacje nietypowe - odstające, to mogą one zaburzać analizę i powinny być usunięte a analiza przeprowadzona ponownie.

• Odległości między punktami wskazują na podobieństwo przypadków - im bliżej (w znaczeniu odległości euklidesowej) zlokalizowane są względem siebie punkty, tym bardziej podobne informacje niosą porównywane przypadki.

• Rzuty prostopadłe punktów na wektory interpretujemy tak samo jak współrzędne punktów, czyli rzuty na osie z tym, że interpretacja dotyczy nie składowych głównych a zmiennych pierwotnych. Wartości umieszczone po stronie końca wektora są większe od średniej wartości zmiennej pierwotnej a wartości umieszczone na przedłużeniu wektora ale w kierunku przeciwnym są wartościami mniejszymi od średniej.